NCERT Solutions Class 12 Computer Science Boolean Algebra have been provided below and is also available in Pdf for free download. The NCERT solutions for Class 12 Computer Science have been prepared as per the latest syllabus, NCERT books and examination pattern suggested in Class 12 by CBSE, NCERT and KVS. Questions given in NCERT book for Class 12 Computer Science are an important part of exams for Class 12 Computer Science and if answered properly can help you to get higher marks. Refer to more Chapter-wise answers for NCERT Class 12 Computer Science and also download more latest study material for all subjects. Boolean Algebra is an important topic in Class 12, please refer to answers provided below to help you score better in exams
Boolean Algebra Class 12 Computer Science NCERT Solutions
Class 12 Computer Science students should refer to the following NCERT questions with answers for Boolean Algebra in Class 12. These NCERT Solutions with answers for Class 12 Computer Science will come in exams and help you to score good marks
Boolean Algebra NCERT Solutions Class 12 Computer Science
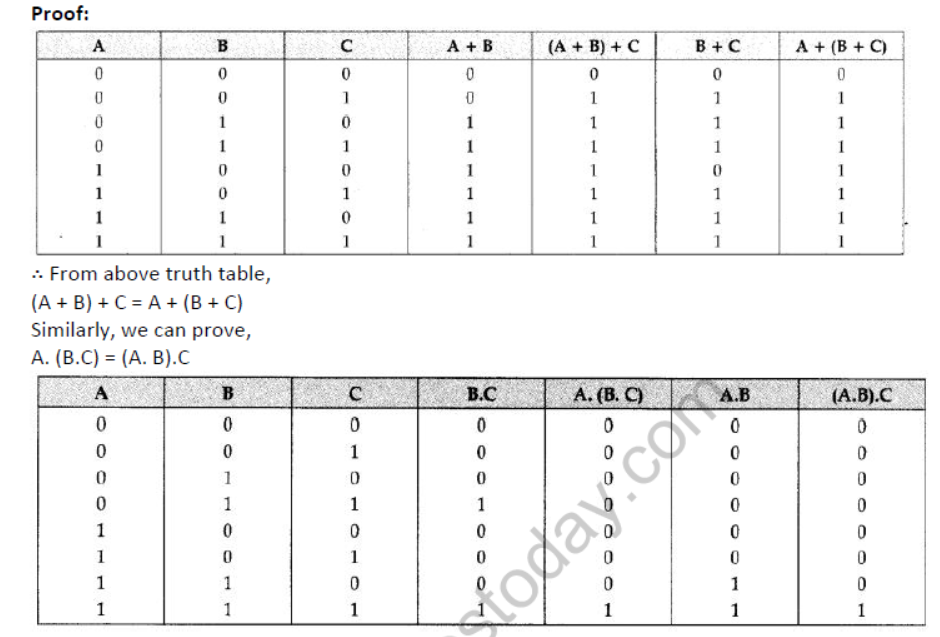
Question 5: State and verify Associative law using Truth Table.
Аnswer: Associative Law: This law states that:
(A + B) + C = A + (B + C)
(A.B).C = A. (B.C)
Short Answer Type Questions-I
Question 1: Correct the following Boolean statements :
1. X+1 = X
2. (A’)’ = A’
3. A+A’ = 0
4. (A+B)’ = A.B
Аnswer:
1. X+l=l or X+0=X
2. ((A’)’) = A
3. A + A’ = 1 or A. A’ = 0
4. (A 4- B)’ = A’.B1
Question 2: Write the POS form of a Boolean Function F, which is represented in a truth table as follows
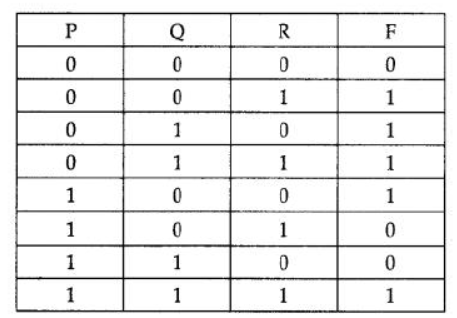
Аnswer:
(P+Q+R).(P’+Q+R).(P’+Q’+R)
Short Answer Type Questions-II
Laws and Theorems
Question 1: State and Verify Absorption law algebraically.
Аnswer: Absorption law states that :
A + AB = A and A. (A + B) = A
Algebraic method :
Taking LHS
A + AB = (A.l) + (A.B) by Identity
= A. (1 + B) by Distribution
= A.l by Null Element
= A
Question 2: State and define principle of duality. Why is it so important in Boolean Algebra ?
Аnswer:
Principle of duality : Duality principle states that from every Boolean relation another Boolean relation can be derived by :
(i) Changing each OR sign (+) to an AND sign (-).
(ii) Changing each AND sign (-) to an OR sign (+)
ex : Dual of A + A’B = A. (A’ + B)
Importance in Boolean Algebra : The principle of duality is an important concept in Boolean algebra, particularly in proving various theorems. The principle of duality is used extensively in proving Boolean algebra theorem. Once we prove that an expression is valid, by the principle of duality, its dual is also valid. Hence, our effort in proving various theorems is reduced to half.
Question 3: Name the law shown below & verify it using a . truth table.

Question 6:
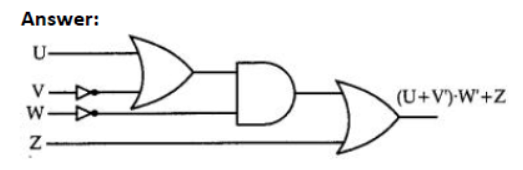
Draw the Logic Circuit for the following Boolean Expression :
(U + V). w + z
Question 7: Verify the following using Boolean Laws :
LT + V = LTV + LP.V + U.V
Аnswer:
L.H.S.
= U’ + V
= U’ . (V + V) + V (LP + U)
= U’ . V + LP . V + U . V + U. V
= U’. V + LP. V + U. V
= R.H.S.
OR
R.H.S.
= U’V’ + U’. V + U. V
= LP . (V + V) + U. V
= U’ 1 + U.V
= U’ + U.V
= U’ +V
= L.H.S.
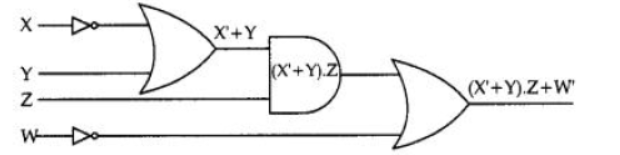
Question 8: Draw the Logic Circuit for the following Boolean Expression :
(X’ + Y). Z + W’
Аnswer:
Question 9: Write the equivalent Boolean expression for the following logic circuit.
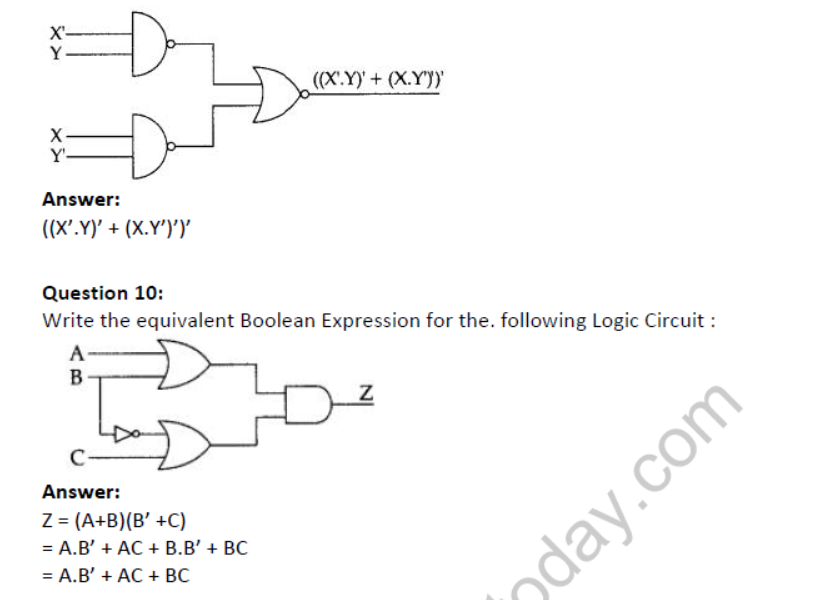


Question 17: Verify the following using Boolean Laws X + Z = X + X’. Z + Y. Z
Аnswer:
Taking RHS
X + X’Z + YZ
= (X + X’). (X + Z) + YZ (Distribution Law)
= 1. (X + Z) + YZ (A + A’ = 1)
= X + Z + YZ
= X + Z (1 + Y)
= X + Z (1 + A = 1; 1. A = A)
= Hence verified
Question 18: Verify the following using Boolean Laws : A + C = A + A. C + B.C
Аnswer:
A + C = A + A’.C + BC
Solve RHS
A + A’C + BC
(A + A). (A + C) + BC [Using distributive law]
1. (A + C) + BC
= A + C + BC
= A + C(1 + B)
= A + C.1
= A + C
= LHS (Hence, verified)
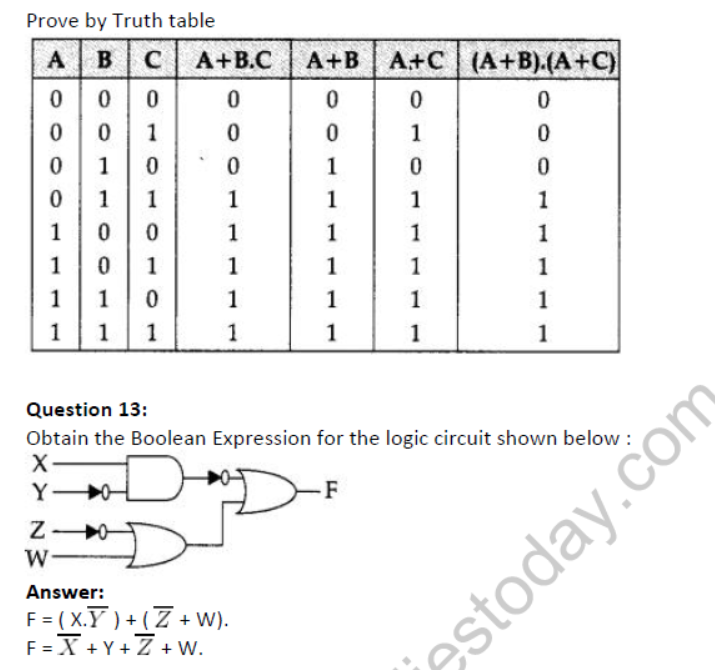
Question 19: Obtain the Boolean Expression for the logic circuit shown below :
Question 24: Derive a Canonical SOP expression for a Boolean function F, represented by the following truth table :
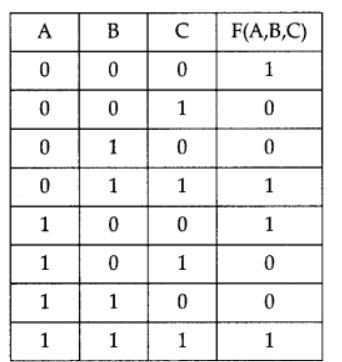
Аnswer:
F(A, B, C) = A’B’C + A’BC + AB’C + ABC
OR
F(A,B,C) =Σ(0, 3,4,7)
Question 25: Derive a Canonical POS expression for a Boolean function F, represented by the following truth table :
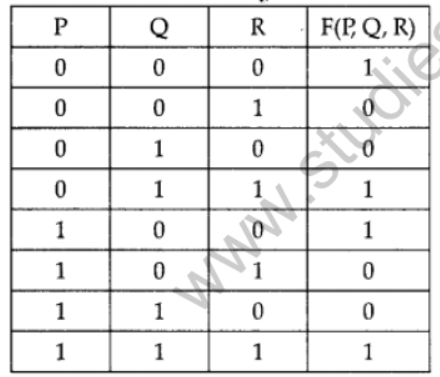
Аnswer:
F(RQ,R) = (P+Q+R’)(P+Q,+R)(P’+Q,+R’) (P’+Q’+R)
OR
F(RQ,R)=II(1,2,5,6)
Question 26: Obtain a simplified form for a Boolean expression :
F(U, V, W, Z) = II (0,1,3,5, 6, 7,15)
Аnswer:
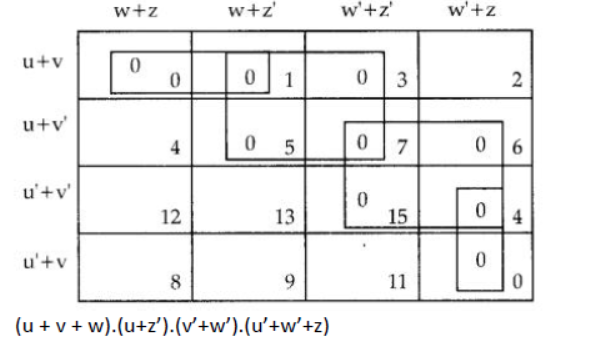
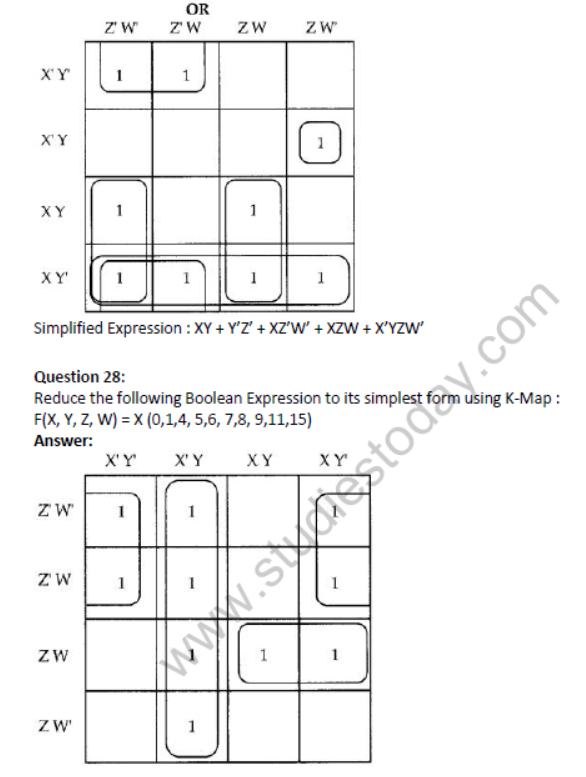
Question 27: Reduce the following Boolean Expression to its simplest form using K-Map :
F (X, X Z, W) = X (0,1, 6, 8, 9,10,11,12,15)
Аnswer:
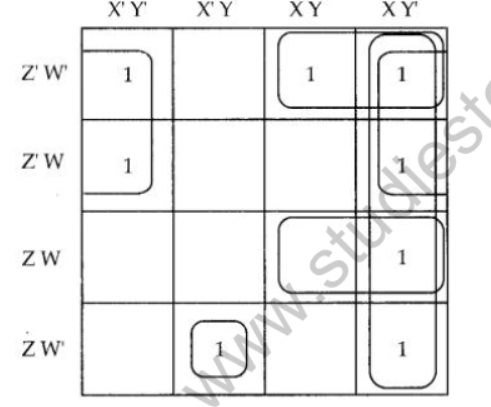
Question 29: Verify the following using Boolean Laws.
X + Y’ = X. Y + X. Y + X’. Y
Аnswer:
L. H. S.
= X + Y’
= X. (Y+Y’) + (X + X’). Y’
= X. Y + X. Y’ + X. Y’ + X’. Y’
= X. Y + X. Y’ + X’. Y’
= R. H. S
OR
= X. Y + X. Y’ + X’. Y’
= X. (Y + Y’) + X’. Y’
= X. 1 + X’. Y’
= X + X’. Y’
= X + Y
= L. H. S
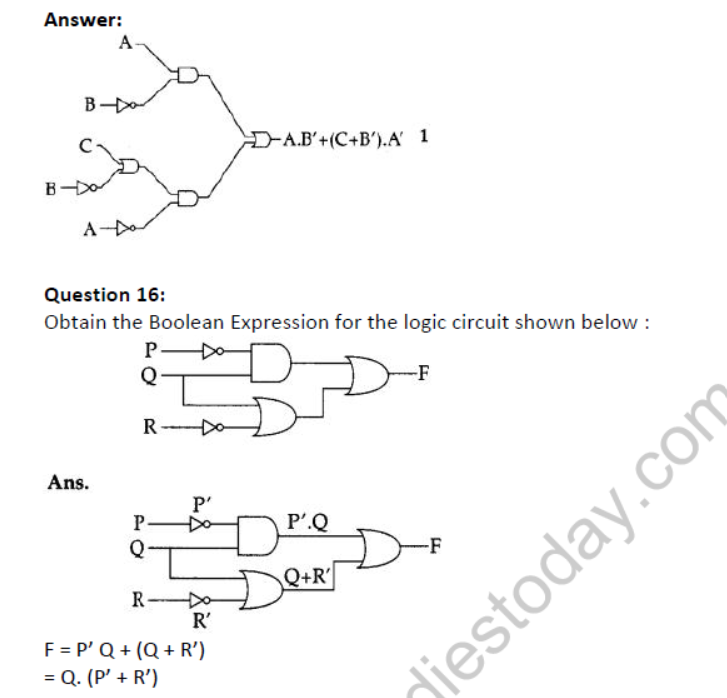
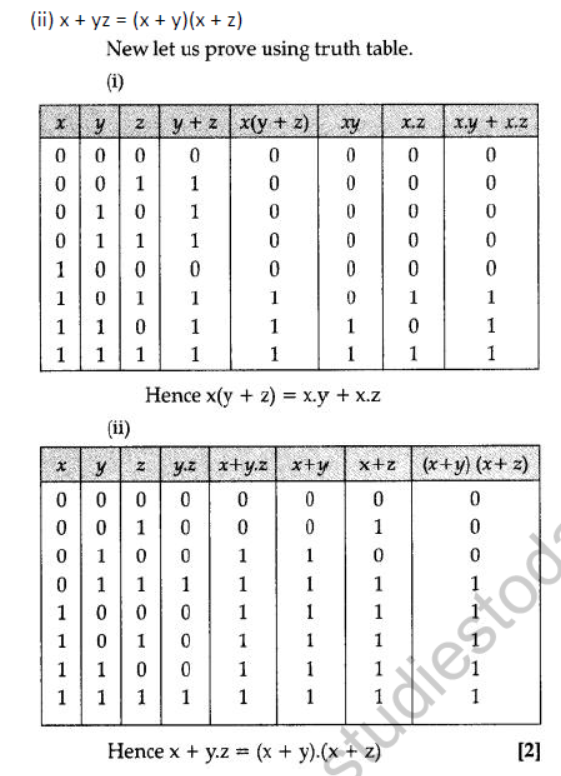
Question 30: State Distributive law and verify it using truth table.
Аnswer:
Distributive law : This law states that
(i) x(y + z) = xy + x.z.
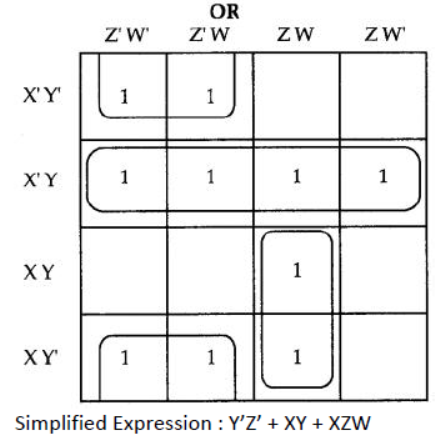
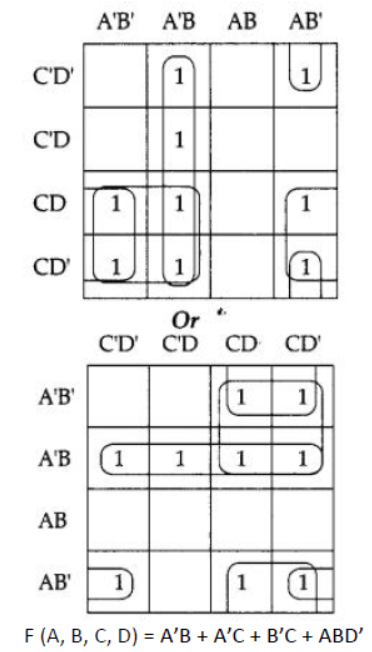
Question 31: Reduce the following Boolean Expression using K Map :
F(A, B, C, D) = Σ{0,1,3, 5, 6, 7,9,11,13,14,15}
Аnswer:
TOPIC-2 Karnaugh Map Minimization and Applications of Boolean Algebra
Very Short Answer Type Questions
Question 1: Write Product of Sum expression of the function F (a, b, c, d) from the given truth table
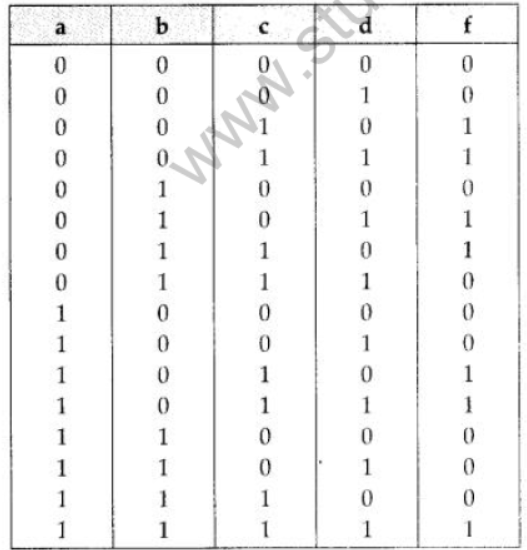
Аnswer:
F (a, b, c, d) =
(a + b + c + d).(a + b + c + d’). (a + b’ + c + d) . (a + b’ + c’ + d’). (a’ + b + c + d).
(a’ + b + c + d’). (a’ + b’ + c + d). (a’ + b’ + c + d’) . (a’ + b’ + c’ + d)
Question 2: Convert the following Boolean expression inti! its equivalent Canonical Sum of Products form (SOP) :
(U + V + W) (U + V + W’) (U’ + V + W) (U’ + V’ + W’)
Аnswer:
π (0,1, 4, 7)
Σ(2, 3, 5, 6)
010 011 101 110
= U’VW’ + U’VW + UV’W + UVW’
Question 3: Write the Sum of Product form of the function F(R Q, R) for the following truth table representation of F :

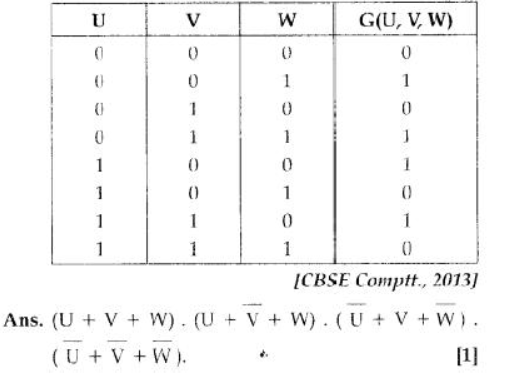
Question 5:Write the Product of Sum form of the function G(U, V W) for the following truth table representation of G :
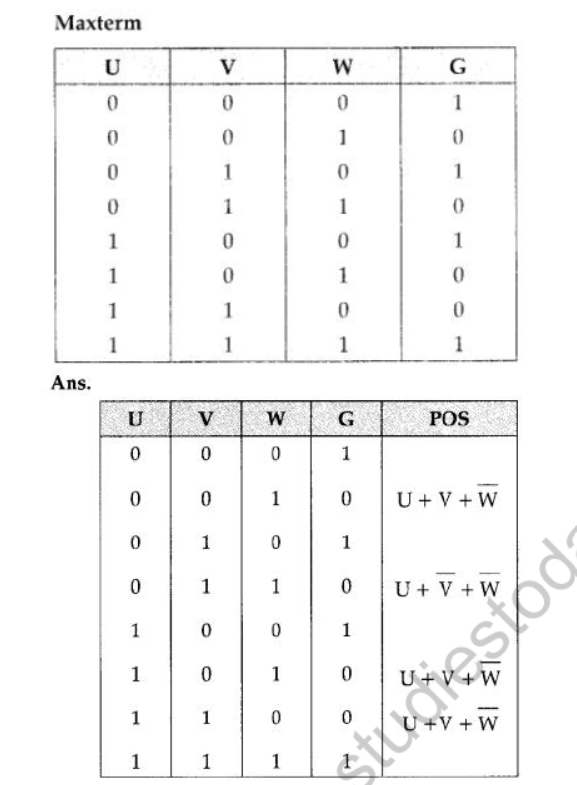
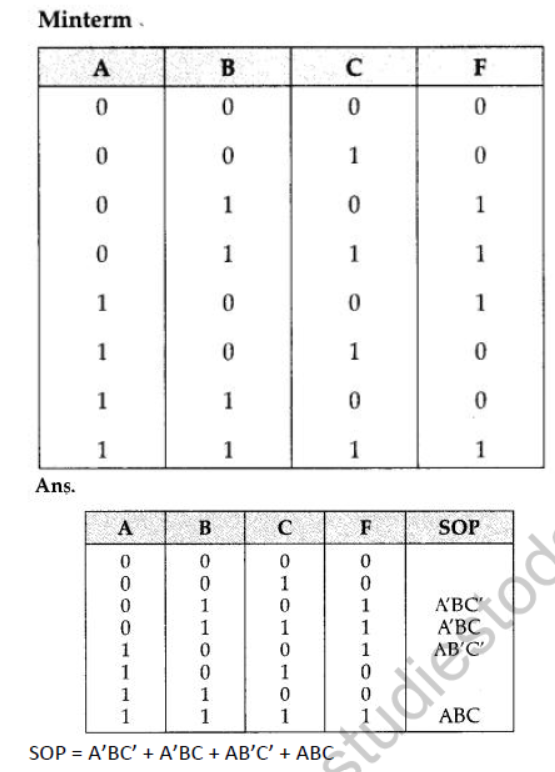
Question 6: Write the Product of Sum form of function G(U, V, W) for the following truth table representation of G :

Question 8: Write the SOP form of a Boolean function F, which is represented in a truth table as follows:
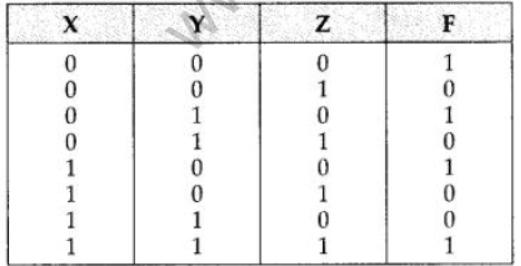
Аnswer:
F(X, Y, Z) = X’.Y’. Z’ + X’. Y. Z’ + X. Y’. Z’+ X.Y.Z
Question 9: Write the POS form of Boolean function G, which is represented in a truth table as follows :
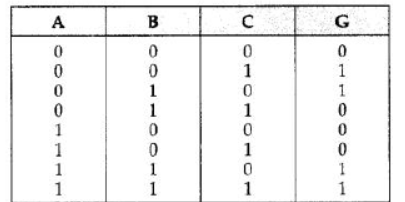
Аnswer:
G (A, B, C) = (A + B + C). (A + B’ + C’). (A’ + B + C). (A’ + B + C’)
Short Answer Type Questions-II
Question 1: Obtain the minimal SOP form for the following Boolean expression using K-Map.
F(A,B,C,D) = Σ (0,2,3,5,7,8,10,1143,15)
Аnswer:
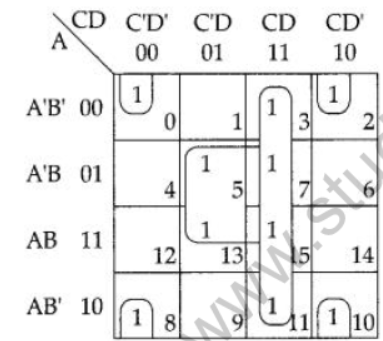
Quad 1 = m0 + m2 + m8 + m10 = B’D’
Quad 2 = m3 + m7 + m15 + m11 = CD
Quad 3 = m5 + m7 + m15 + m13 = BD
Minimal SOP = B’D’ + CD + BD
Question 2: Reduce the following Boolean expression using
K-Map :
F(A,B,C,D) = 7r (0,1,2,4,5,6,8,10)
Аnswer:
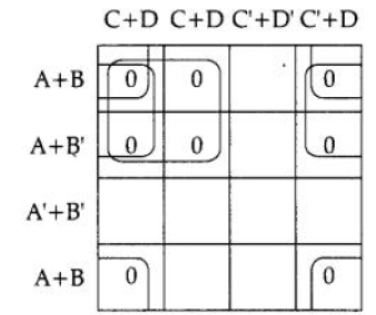
F(A, B, C, D) = π(0,1,2,4, 5, 6,8,10) F = (A + C).(A + D).(B + D)
Question 3: Reduce the following using K-Map :
F (A, B,C,D) = Σ(1,3,4,5,6,7,12,13)
Аnswer:
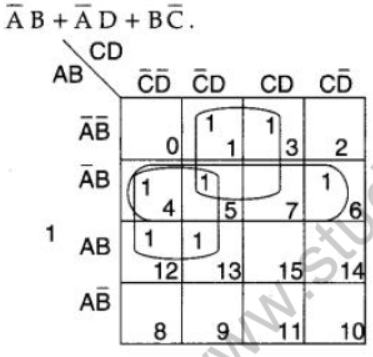
Question 4: Reduce the following Boolean expression using K-map.
F(EQ,R,S) = 2(0,2,4,5,6,7,8,10,13,15).
Аnswer:
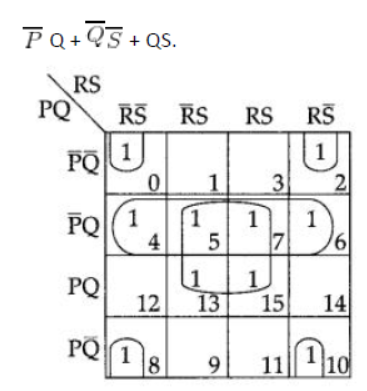
Question 5: Reduce the following Boolean Expression using K-Map :
F(P, Q, R, S) = Σ(1,2, 3,4,5, 6, 7, 8,10)
Аnswer:
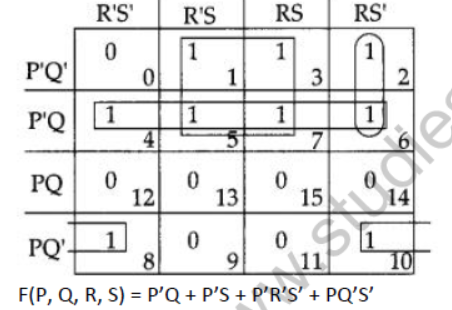
Question 6: Reduce the following Boolean Expression using
K-Map :
F (A, B, C, D) = Σ(2, 3,4,5, 6, 7,8,10,11)
Long Answer Type Questions
Question 1: Verify the following using Boolean Laws :
A ‘ + B’ . C=A’ . B ‘ . C ‘ + A’ . B . C ‘ + A’ .B.C + A’ .B’ .C+ A.B’ .C
Аnswer:
A’+ B’C = A’B’C’ + A,BCI + A’BC’ + A’BC + A’B’C + ABC
=A’C'(B’+B)+A’C (Grouping)
(B+B’)+AB’C
=> A’C’+ A’C + AB’C
(x+x’y=x+y)
=> A’ (C+C’ ) +AB’ C
=> A’+AB’C
(x+x’=1)
=> A’+B’C
X=A’ y=B’C
= LHS
Hence Proved.
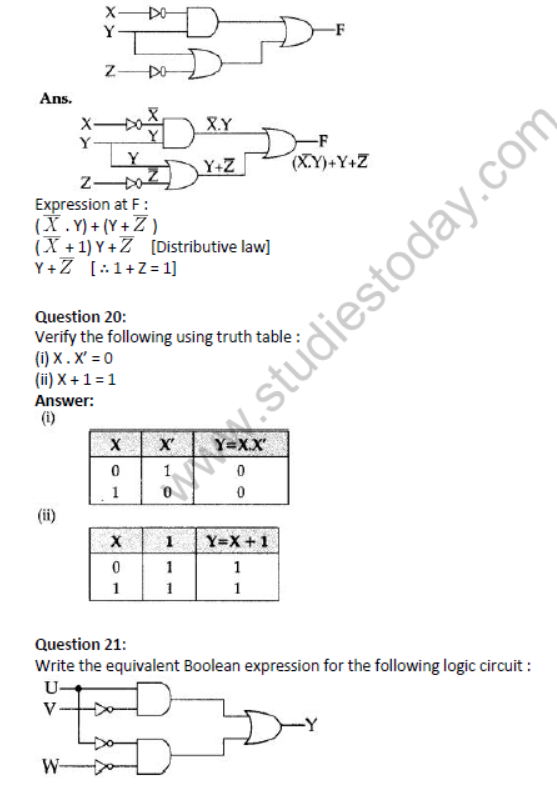
Question 2: Write the Boolean Expression for the result of the Logic Circuit as shown below :
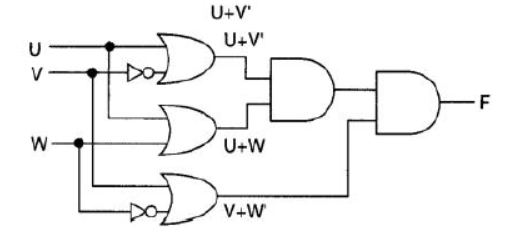
Аnswer:
F = (u+v’).(u+w).(v+w’)
Question 3: Derive a Canonical POS expression for a Boolean function F, represented by the following truth table :
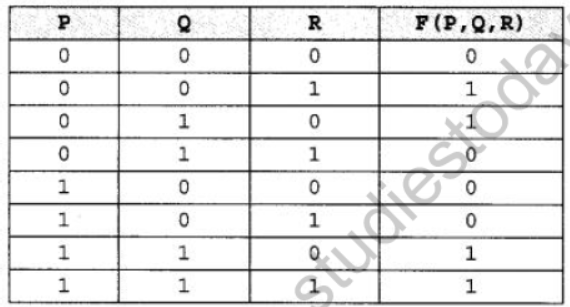
Аnswer:
F = Σ(0, 3,4,5)
= (P + Q + R) (P + Q’ + R’) (P’ + Q + R) (P’ + Q + R’)
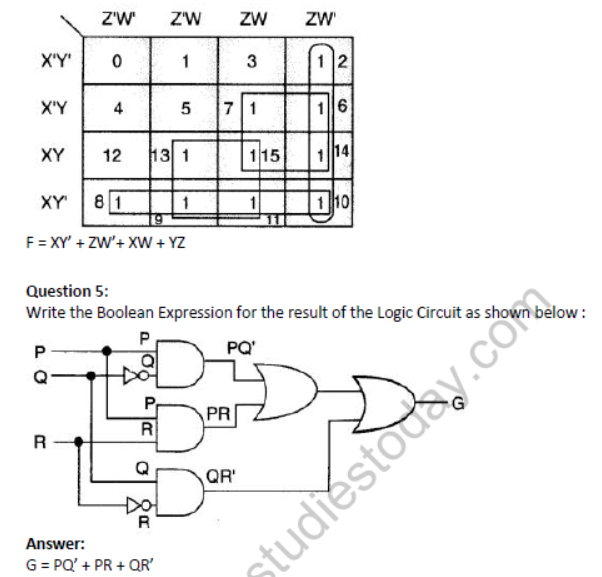
Question 4: Reduce the following Boolean Expression to its simplest form using K-Map :
F (X, Y, Z, W)
Σ(2,6,7,8,9,10,11,13,14,15)
Аnswer:
Σ(2,6,7,8,9,10,11,13,14,15)
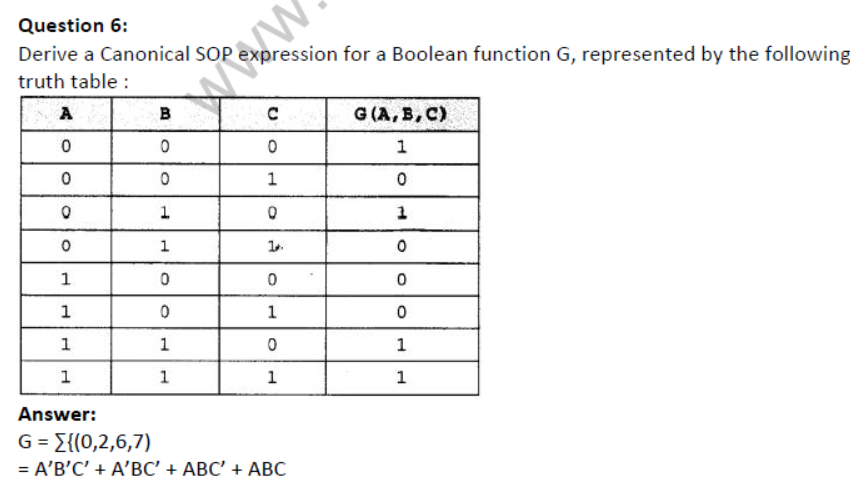
Question 7: Verify the following using Boolean Laws :
X’+ Y’Z = X’ .Y’ .Z’+X’ .Y.Z’+X’ .Y.Z+X’ .Y’ .Z + X.Y’.Z.
Аnswer:
X ‘+Y’ Z=X ‘ Y ‘ Z ‘ +X ‘ YZ ‘ +X ‘ YZ+X ‘ Y ‘ Z+XY ‘ Z
Taking RHS
Grouping terms
=> x’Z’ (Y’+Y)+X’ Z(Y+Y’)+XY’Z
=> X’Z’+X’Z+XY’Z
(Y+Y’=1)
=> X'(Z’+Z)+XY’Z
(Grouping)
=> X’+XY’Z (Z+Z’=l)
=> X’+Y’Z (Substitute X=X’ Y=Y’Z X+X’ Y = X+Y)
= LHS
Question 8: Reduce the following Boolean Expression to its simplest form using K-Map :
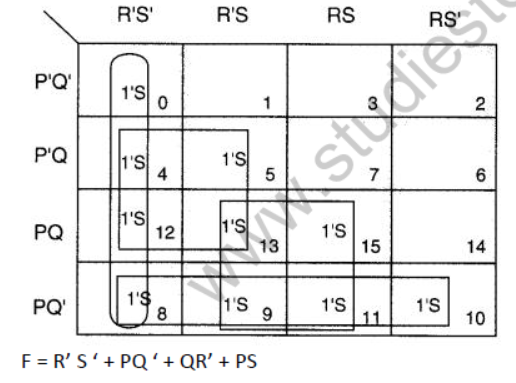
F(P,Q,R,S) = Σ(0,4,5,8,9,10,11,12,13,15)
Аnswer: F(P,Q,R,S) = Σ(0,4,5,8,9,10,11,12,13,15)
| NCERT Solutions Class 12 Computer Science Chapter 3 Stack |
| NCERT Solutions Class 12 Computer Science Chapter 4 Queue |
| NCERT Solutions Class 12 Computer Science Chapter 8 Database Concepts |
| NCERT Solutions Class 12 Computer Science Chapter 9 Structured Query Language |
NCERT Solutions Class 12 Computer Science Boolean Algebra
The above provided NCERT Solutions Class 12 Computer Science Boolean Algebra is available on our website for free download in Pdf. You can read the solutions to all questions given in your Class 12 Computer Science textbook online or you can easily download them in pdf. The answers to each question in Boolean Algebra of Computer Science Class 12 has been designed based on the latest syllabus released for the current year. We have also provided detailed explanations for all difficult topics in Boolean Algebra Class 12 chapter of Computer Science so that it can be easier for students to understand all answers. These solutions of Boolean Algebra NCERT Questions given in your textbook for Class 12 Computer Science have been designed to help students understand the difficult topics of Computer Science in an easy manner. These will also help to build a strong foundation in the Computer Science. There is a combination of theoretical and practical questions relating to all chapters in Computer Science to check the overall learning of the students of Class 12.
You can download the NCERT Solutions for Class 12 Computer Science Boolean Algebra for latest session from StudiesToday.com
Yes, the NCERT Solutions issued for Class 12 Computer Science Boolean Algebra have been made available here for latest academic session
Regular revision of NCERT Solutions given on studiestoday for Class 12 subject Computer Science Boolean Algebra can help you to score better marks in exams
Yes, studiestoday.com provides all latest NCERT Boolean Algebra Class 12 Computer Science solutions based on the latest books for the current academic session
Yes, NCERT solutions for Class 12 Boolean Algebra Computer Science are available in multiple languages, including English, Hindi
All questions given in the end of the chapter Boolean Algebra have been answered by our teachers

