Exercise 9.1
Question 1: Express each of the following in the language of ratios:
(i) In a class, the number of girls in the merit list of the board examination is two times that of boys.
(ii) The number of students passing mathematics test is 2/3 of the number that appeared.
Solution 1:
(i) It is given that the number of girls in the merit list of the board examination is two times that of boys.
Therefore, the ratio of number of girls and boys in the merit list is 2∶ 1.
(ii) It is given that the number of students passing mathematics test is 2/3 of the number that appeared.
Therefore, the ratio of the number of students passing a mathematics test out of total students is 2∶3.
Question 2: Express the following ratios in language of daily life:
(i) The ratio of the number of bad pencils to that of good pencils produced in a factory is 1: 9.
(ii) In India, the ratio of the number of villages to that of cities is about 2000: 1.
Solution 2:
(i) Bad pencils produced in a factory is 1/9 of the good pencils produced in the factory.
(ii) Number of villages is 2000 times of cities in India.
Question 3: Express each of the following ratios in its simplest form:
(i)60∶72
(ii)324∶144
(iii)85∶391
(iv)186∶403
Solution 3:

Question 4: Find the ratio of the following in the simplest form:
(i) 75 paise to Rs. 3
(ii) 35 minutes to 45 minutes
(iii) 8 kg to 400gm
(iv) 48 minutes to 1 hour
(v) 2 metres to 35 cm
(vi) 35 minutes to 45 seconds
(vii) 2 dozen to 3 scores
(viii) 3 weeks to 3 days
(ix) 48 min to 2 hours 40 min
(x) 3 m 5 cm to 35 cm
Solution 4:
(i) 75 paise to Rs. 3
75 paise : Rs. 3
Rs. 1 = 100 paise
Rs. 3 = 300 paise
We can write it as
75 paise : Rs. 3 = (75 paise)/(300 paise)
HCF of 75 and 300 is 75.
Dividing the numerator and denominator by HCF 75.
(75 paise ÷ 75)/(300 paise ÷ 75)= 1/4
Hence, the ratio of 75 paise to Rs. 3 is 1:4.
(ii) 35 minutes to 45 minutes
35 minutes to 45 minutes = 35 minutes : 45 minutes
35 minutes : 45 minutes = (35 minutes)/(45 minutes)
HCF of 35 and 45 is 5.
Dividing the numerator and denominator by HCF 5.
(35 minutes ÷ 5)/(45 minutes ÷ 5)=7/9
Hence, the ratio of 35 minutes to 45 minutes is 7:9.
(iii) 8 kg to 400gm
1 kg = 1000 gm
8 kg = 8000 gm
8 kg to 400 gm = 8000 gm : 400 gm
HCF of 8000 and 400 is 400.
Dividing the numerator and denominator by HCF 400.
(8000 Kg ÷ 400)/(400 Kg ÷ 400)=20/1
Hence, the ratio of 8000 gm to 400 gm 20 : 1.
(iv) 48 minutes to 1 hour
1 hour = 60 minutes
48 minutes to 1 hour = 48 minutes: 60 minutes
HCF of 48 and 60 is 12.
Dividing the numerator and denominator by HCF 12.
(48 ÷ 12)/(60 ÷ 12)=4/5
Hence, the ratio of 48 minutes to 1 hour 4 : 5.
(v) 2 metres to 35 cm
1 m = 100 cm
2 metres = 200cm
2 metres to 35 cm = 200 cm: 35 cm
HCF of 200 and 35 is 5.
Dividing the numerator and denominator by HCF 5.
(200 ÷ 5)/(35 ÷ 5)=40/7
Hence, the ratio of 2 metres to 35 cm is 40 : 7.
(vi) 35 minutes to 45 seconds
1 min. = 60 sec.
35 minutes = 2100 seconds
35 minutes to 45 seconds = 2100 seconds: 45 seconds
HCF of 2100 : 45 is 15.
Dividing the numerator and denominator by HCF 15.
(2100 ÷ 15)/(45 ÷ 15) = 140/3
Hence, the ratio of 35 minutes to 45 seconds is 140 : 3.
(vii) 2 dozen to 3 scores
1 dozen = 12
1 score = 20
2 dozen = 2 × 12 = 24
2 scores = 2 × 20 = 40
2 dozen to 3 scores = 24 : 60
HCF of 24 and 60 is 12.
Dividing the numerator and denominator by HCF 12.
(24 ÷ 12)/(60 ÷ 12) = 2/5
Hence, the ratio of 2 dozen to 3 scores is 2 : 5.
(viii) 3 weeks to 3 days
1 week = 7 days
3 week = 21 days
3 weeks to 3 days = 21 days : 3 days
HCF of 21 and 3 is 3.
Dividing the numerator and denominator by HCF 3.
(21÷3)/(3÷3)=7/1
Hence, the ratio of 3 weeks to 3 days is 7: 1.
(ix) 48 min to 2 hours 40 min
1 hour = 60 min
2 hour = 120 min
48 min to 2 hours 40 min = 48 min : 120 min + 40 min
48 min to 2 hours 40 min = 48 min : 160 min
HCF of 48 and 160 is 16.
Dividing the numerator and denominator by HCF 16
(48÷16)/(160÷16)=3/10
Hence, the ratio of 48 min to 2 hours 40 min is 3: 10.
(x) 3 m 5 cm to 35 cm
1 m = 100 cm
3 m = 300 cm
3 m 5 cm to 35 cm = 3 m 5 cm: 35 cm
3 m 5 cm to 35 cm = 300cm + 5 cm: 35 cm
3 m 5 cm to 35 cm = 305cm : 35 cm
HCF of 305 and 35 is 5.
Dividing the numerator and denominator by HCF 5.
(305÷5)/(35÷5)=61/7
Hence, the ratio of 3 m 5 cm to 35 cm is 61: 7.
Question 5: Find the ratio of
(i) 3.2 metres to 56 metres
(ii) 10 metres to 25 cm
(iii) 25 paise to Rs. 60
(iv) 10 litres to 0.25 litre
Solution 5:
(i) 3.2 metres to 56 metres
1 m = 100 cm
3 m = 300 cm
We can write it as
3.2 metres : 56 metres = (3.2 metres)/(56 metres)
For removing decimal from numerator we get
(3.2 × 10)/(56 × 10)= 32/560
HCF of 32 and 560 is 16.
Dividing the numerator and denominator by HCF 16.
(32÷16)/(560÷16)=2/35
Hence, the ratio of 3.2 metres to 56 metres is 2 : 35.
(ii) 10 metres to 25 cm
1 m = 100 cm
10 m = 1000 cm
We can write it as
10 metres : 25 cm = 10 m : 25 cm
10 metres : 25 cm = (1000 cm)/(25 cm)
Dividing the numerator and denominator by HCF 25.
(1000 ÷ 25)/(25 ÷ 25)=40/1
Hence, the ratio of 10 metres to 25 cm is 40 : 1.
(iii) 25 paise to Rs. 60
Re 1 = 100 paise
Rs. 60 = 6000 paise
We can write it as
25 paise : Rs. 60 = 25 paise : Rs. 60
25 paise : Rs. 60 = (25 paise)/(6000 paise)
HCF of 25 and 6000 is 25.
Dividing the numerator and denominator by HCF 25
(25 ÷ 25)/(6000 ÷ 25)=1/240
Hence, the ratio of 25 paise to Rs. 60 is 1 : 240.
(iv) 10 litres to 0.25 litre
10 litres to 0.25 litre = 10 litres : 0.25 litre
10 litres to 0.25 litre = (10 litres)/(0.25 litres)
For removing decimal from numerator we get
(10 × 100)/(0.25 × 100)= 1000/25
HCF of 1000 and 25 is 25.
Dividing the numerator and denominator by HCF 25.
(1000 ÷ 25)/(25 ÷ 25)=40/1
Hence, the ratio of 10 litres to 0.25 litre is 40 : 1.
Question 6: The number of boys and girls in a school are 1168 and 1095 respectively. Express the ratio of the number of boys to that of the girls in the simplest form.
Solution 6:
Number of boys in school = 1168
Number of girls in school = 1095
The ratio of the number of boys and girls = 1168 : 1095
HCF of 1168 and 1095 is 73.
Dividing the numerator and denominator by HCF 73.
(1168÷73)/(1095÷73)=16/15
Thus, the ratio of the number of boys to that of girls in simplest form is 16: 15.
Question 7: Avinash works as a lecturer and earns Rs 12000 per month. His wife who is a doctor earns Rs 15000 per month. Find the following ratios:
(i) Avinash’s income to the income of his wife.
(ii) Avinash’s income to their total income.
Solution 7:
Salary of Avinash earned every month = Rs. 12,000
Salary of Avinash’s wife salary per month = Rs. 15000
(i) Avinash’s income to the income of his wife = 12000/15000
HCF of 12000 and 15000 is 3000.
Avinash’s income to the income of his wife = (12000 ÷ 3000)/(15000 ÷ 3000)=4/5
Avinash’s income to the income of his wife = 4: 5
(ii) Total income = 12,000 + 15,000 = 27,000
Avinash’s income to their total income = 12000/15000
HCF of 12000 and 27000 is 3000.
Avinash’s income to their total income = (12000 ÷ 3000)/(27000 ÷ 3000)=4/9
Avinash’s income to their total income = 4 : 9
Question 8: Of the 72 persons working in an office, 28 are men and the remaining are women. Find the ratio of the number of:
(i) men to that of women,
(ii) men to the total number of persons
(iii) persons to that of women.
Solution 8:
Total Number of persons in an office = 72
Number of men’s = 28
Number of women = 72 – 28 = 44
(i) The ratio of men to that of women is 28 : 44.
HCF of 28 and 44 is 4.
Dividing the numerator and denominator by HCF 4.
Men to that of women = (28 ÷ 4)/(44 ÷ 4)=7/11
Hence, the ratio of men to that of women is 7 : 11.
(ii) The ration of Men to the total number of persons = 28: 72
HCF of 28 and 72 is 4.
Dividing the numerator and denominator by HCF 4.
Men to the total number of persons = (28 ÷ 4)/(72 ÷ 4)=7/18
Hence, the ratio of men to the total number of persons is 7 : 18.
(iii) The ratio of persons to that of women = 72 : 44
HCF of 72 and 44 is 4.
Dividing the numerator and denominator by HCF 4.
Persons to that of women = (72 ÷ 4)/(44 ÷ 4)=18/11
Hence, the ratio of total persons to that of women is 18 : 11.
Question 9: The length of a steel tape for measurements of buildings is 10 m and its width is 2.4 cm. What is the ratio of its length to width?
Solution 9:
Length of a steel tape = 10 m
Width of steel tape = 2.4 cm
1 m = 100 cm
Ratio of its length to width = (10 m)/(2.4 cm)
Ratio of its length to width = (1000 cm)/(2.4 cm)
For removing decimal from numerator we get
(1000 × 10)/(2.4 × 10)= 10000/24
HCF of 10000 and 24 is 8.
Dividing the numerator and denominator by HCF 8.
(1000 ÷ 8)/(24 ÷ 8)=1250/3
The Ratio of length to width = 1250 : 3
Thus, the ratio of its length to width is 1250 : 3.
Question 10: An office opens at 9 am and closes at 5 pm with a lunch interval of 30 minutes. What is the ratio of lunch interval to the total period in office?
Solution 10:
Opening time of office = 9am
Closing time of office = 5pm
Total Duration of office = 9 am to 5 pm = 8 hours
1 hour = 60 minutes
8 hour = 480 minutes
Lunch interval = 30 minutes
The ratio of lunch interval to the period in office = (30 minutes)/(8 hours)
The ratio of lunch interval to the period in office = (30 minutes)/(480 minutes)
HCF of 30 and 480 is 30.
Dividing the numerator and denominator by HCF 30.
(30 ÷30)/(480 ÷30) = 1/16
Thus, the Ratio of lunch interval to the total period is 1 : 6.
Question 11: A bullock-cart travels 24 km in 3 hours and a train travels 120 km in 2 hours. Find the ratio of their speeds.
Solution 11:
It is given that,
The Distance travelled by bullock-cart = 24 km in 3 hours
The Distance travelled by train = 120 km in 2 hours
Distance travelled by bullock-cart per km = (24 km)/3
Distance travelled by bullock-cart per km = 8 km
Distance travelled by train per km = (120 km)/2
Distance travelled by train per km = 60 km
Ratio of their speeds = 8/60
HCF of 8 and 60 is 4.
Dividing the numerator and denominator by HCF 4.
(8 ÷ 4)/(60 ÷4) = 2/15
Thus, the Ratio of their speeds is 2 : 15.
Question 12: Margarette works in a factory and earns Rs. 955 per month. She saves Rs. 185 per month from her earnings. Find the ratio of:
(i) her savings to her income
(ii) her income to her expenditure.
(iii) her savings to her expenditure.
Solution 12:
Monthly income of Margarette = Rs. 955
Monthly savings of Margarette = Rs. 185
Monthly Expenditure of Margarette = 955 – 185 = Rs. 770
(i) her savings to her income = 185/955
HCF of 185 and 955 is 5.
Dividing the numerator and denominator by HCF 5.
(185÷5)/(955÷5)=37/191
Thus, the ratio of her savings to her income is 37: 191.
(ii) her income to her expenditure = 955/770
HCF of 955 and 770 is 5.
Dividing the numerator and denominator by HCF 5.
(955 ÷ 5)/(770 ÷ 5)=191/154
Thus, the ratio of income to her expenditure is 191: 154.
(iii) her savings to her expenditure = 185/770 = 37: 154
HCF of 185 and 770 is 5.
Dividing the numerator and denominator by HCF 5.
(185 ÷ 5)/(770 ÷ 5)=37/154
Thus, the ratio of savings to her expenditure is 37 : 154.
Exercise 9.2
Question 1: Which ratio is larger in the following pairs?
(i) 3: 4 or 9: 16
(ii) 15: 16 or 24: 25
(iii) 4: 7 or 5: 8
(iv) 9: 20 or 8: 13
(v) 1: 2 or 13: 27
Solution 1:
Exercise 9.3
Question 1: Which of the following statements are true?
(i) 16 : 24 = 20 : 30
(ii) 21 : 6 = 35 : 10
(iii) 12 : 18 = 28 : 12
(iv) 51 : 58 = 85 : 102
(v) 40 men : 200 men = Rs. 5 : Rs. 25
(vi) 99 kg : 45 kg = Rs. 44 : Rs. 20
Solution 1:
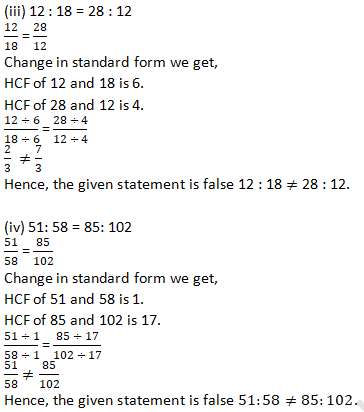
Question 2: Find which of the following are in proportion:
(i) 8, 16, 6, 12
(ii) 6, 2, 4, 3
(iii) 150, 250, 200, 300
Solution 2:
Question 3: Find x in the following proportions:
(i) x∶ 6 = 55∶ 11
(ii) 18∶ x = 27∶ 3
(iii) 7∶ 14 = 15∶ x
(iv) 16∶ 18 = x∶ 96
Solution 3:
Question 4: Set up all proportions from the numbers 9, 150, 105, 1750.
Solution 4: Below are the possible proportions for the given numbers.

Question 5: Find the other three proportions involving terms of each of the following:
(i) 45 : 30 = 24 : 16
(ii) 12 : 18 = 14 : 21
Solution 5:


Question 6: If 4, x, 9 are in continued proportion, find the value of x.
Solution 6:
It is given that 4, x, 9 are in continued proportion
4∶ x∷x∶ 9
4/x = x/9
By cross multiplication we get,
x2=4×9
x2=36
x=√36
x=6
Hence, the continued proportion is 6.
Question 7: If in a proportion, the first, second and fourth terms are 32, 112 and 217 respectively, find the third term.
Solution 7:
The first, second and fourth terms are 32, 112 and 217.
Let the third term which is missing term be x
32: 112 :: x: 217
32/112 = x/217
112×x=32×217
112×x=6944
x=6944/112
x=62
Hence, the third is 62.
Question 8: Show that the following numbers are in continued proportion:
(i) 36, 90, 225
(ii) 48, 60, 75
(iii) 16, 84, 441
Solution 8:
(i) 36, 90, 225
We can write is that 36 : 90 :: 90 : 225
36/90=90/225
Change in standard from we get,
2/5=2/5
Hence, 36: 90 :: 90: 225 is continue proportion.
(ii) 48, 60, 75
We can write is that 48 : 60 :: 60 : 75
48/60=60/75
Change in standard from we get,
4/5=4/5
Hence, 48: 60 :: 60: 75 is continue proportion.
(iii) 16, 84, 441
We can write is that 16 : 84 :: 84 : 441
16/84=84/441
Change in standard from we get,
4/21=4/21
Hence, 16: 84 :: 84: 441 is continue proportion.
Question 9: The ratio of the length of a school ground to its width is 5: 2. Find its length if the width is 40 metres.
Solution 9:
Ratio between the length of a school ground and its width is = 5 : 2
Width of the school ground = 40 m
Length of the school ground = 40× 5/2=100m
Thus, the length of the school ground is 100 m.
Question 10: The ratio of the sale of eggs on a Sunday to that of the whole week of a grocery shop was 2 : 9. If the total sale of eggs in the same week was Rs. 360, find the sale of eggs on Sunday.
Solution 10:
Ratio between sale of eggs on a Sunday to the whole week is = 2 : 9
Let us assume that, sale of eggs be x
Sales of eggs on Sunday = 2x
Sales of eggs in a week = 9x
Sale of eggs in a week = Rs. 360
9x=360
x=360/9
x=40
Sales of eggs on Sunday = 2x
Sales of eggs on Sunday = 2×40
Sales of eggs on Sunday = Rs.80
Hence, the value of eggs sold on Sunday is Rs. 80.
Question 11: The ratio of copper and zinc in an alloy is 9: 7. If the weight of zinc in the alloy is 9.8 kg, find the weight of copper in the alloy.
Solution 11:
We have,
The Ratio of copper and zinc in an alloy = 9 : 7
Weight of zinc in alloy = 9.8kg
Let us assumed that weight of copper in alloy is = 9x
Weight of zinc in alloy = 7x
7x=9.8kg
x=9.8/7 kg
x=9.8/7 kg
x=1.4kg
Weight of copper = 9×x
Weight of copper = 9×1.4
Weight of copper = 12.6 kg
Hence, the weight of copper in the alloy is 12.6 kg.
Question 12: The ratio of the income to the expenditure of a family is 7: 6. Find the savings if the income is Rs. 1400.
Solution 12:
The income to the expenditure ratio of a family is = 7 : 6
Let us assumed that income of a family is = 7x
and expenditure is = 6x
Saving Ratio = Total Income – Expenditure
=7x – 6x
= x
Total income of the family is = Rs. 1400
Income of a family is = 7x
7x=1400
x=1400/7
x=200
Hence, the saving of the family is Rs. 200.
Question 13: The ratio of story books in a library to other books is 1 : 7. The total number of story books is 800. Find the total number of books in the library.
Solution 13:
The Story books in a library to other books ratio is = 1 : 7
Let us assumed that, the number of story books is = 1x
Number of other books is = 7x
Total number of story books = 800
Ratio of Story books = 1x
1x=800
x=800
Number of other books = 7x
Number of other books = 7×x
Number of other books = 5600
Total number of books = Story Books + Other Books
Total number of books = 5600 + 800
Total number of books = 6400
Thus, Total number of books in the library is 6400.
Exercise 9.4
Question 1: The price of 3 metres of cloth is Rs. 79.50. Find the price of 15 metres of such cloth.
Solution 1:
The price of 3m cloth = Rs. 79.50
1 m cloth price = 79.50/3 = Rs. 26.5
Price of 15 m of cloth = 26.5 × 15
Price of 15 m of cloth = Rs. 397.50
Thus, the price of 15 m cloth is Rs 397.50.
Question 2: The cost of 17 chairs is Rs. 9,605. Find the number of chairs that can be purchased in Rs. 56,500.
Solution 2:
Cost of 17 chairs = Rs. 9,605
Cost of 1 chair = 9,605/17=Rs.565
Number of chairs purchased in Rs. 56,500 is = (Rs. 56,500)/(Rs. 565)
Number of chairs purchased in Rs. 56,500 is = 100
Thus, 100 chairs can be purchased in Rs. 56,500.
Question 3: Three ferry loads are needed to carry 150 people across a river. How many people will be carried on 4 ferry loads?
Solution 3:
People required to carry 3 ferry loads = 150
People required to carry 1 ferry load = 150/3
People required to carry 1 ferry load = 50
Number of people required to carry 4 ferry loads = 4 × 50
Number of people required to carry 4 ferry loads = 200
Thus, 200 people are required to carry 4 ferry loads.
Question 4: If 9 kg of rice costs Rs. 120.60, what will 50 kg of such a quality of rice cost?
Solution 4:
Cost of 9kg rice = Rs. 120.60
Cost of 1kg rice = (Rs. 120.60)/9
Cost of 1kg rice = Rs. 13.4
Cost of 50kg rice = Rs. 13.4 × 50
Cost of 50kg rice = Rs. 670
Thus, 50 kg of such a quality of rice costs Rs. 670.
Question 5: A train runs 200 kilometres in 5 hours. How many kilometres does it run in 7 hours?
Solution 5:
Distance travelled by train in 5 hours = 200km
Distance travelled by train in 1 hour = 200/5
Distance travelled by train in 1 hour = 40km
Distance travelled by train in 7 hours = 40 × 7
Distance travelled by train in 7 hours = 280km
Thus, the train runs 280 km in 7 hours.
Question 6: 10 boys can dig a pitch in 12 hours. How long will 8 boys take to do it?
Solution 6:
It is given that,
10 boys can dig a pitch in = 12 hours
Time taken by 1 boy = 10 × 12 = 120 hours
Time taken by 8 boys to dig the pitch = 120/8
Time taken by 8 boys to dig the pitch = 15 hours
Thus, 8 boys will take 15 hours to dig the pitch.
Question 7: A man can work 8 hours daily and finishes a work in 12 days. If he works 6 hours daily, in how many days will the same work be finished?
Solution 7:
If a man can work only 1 hour, then the time taken to finish the work = 8 × 12
If he works for one hour, then the time taken to finish the work = 96 days
Numbers of days required to finish the woke by 6 hours of working = 96/6
Numbers of days required to finish the woke by 6 hours of working = 16 days
Thus, Numbers of days required by the man for finish the work is 16 days.
Question 8: Fifteen post cards cost Rs. 2.25. What will be the cost of 36 post cards? How many postcards can be bought in Rs. 45?
Solution 8:
15 post cards cost = Rs. 2.25
One Postcard cost = Rs. 2.25/15
One Postcard cost = Rs. 0.15
Cost of 36 post cards = Rs. 0.15 × 36
Cost of 36 post cards = Rs 5.40
We know that,
The Cost of 1 post card = Rs. 0.15
Number of postcards can be purchased in Rs. 45 = (Rs.45)/(Rs. 0.15)
Number of postcards can be purchased in Rs. 45 = 300
Thus, Rs. 5.40 cost of 36 post cards and 300 postcards can be bought in Rs 45.
Question 9: A rail journey of 75 km costs Rs. 215. How much will a journey of 120 km cost?
Solution 9:
Cost of rail journey of 75km = Rs. 215
Cost of rail journey of 1 km = Rs. 215/75
Cost of rail journey of 1 km = Rs. 2.87
The cost of rail journey of 120 km = Rs.2.87× 120
The cost of rail journey of 120 km = Rs. 344
Thus, the cost of rail journey of 120 km is Rs 344.
Question 10: If the sales tax on a purchase worth Rs 60 is Rs 4.20. What will be the sales tax on the purchase worth Rs 150?
Solution 10:
Sales tax on a purchase worth Rs. 60 = Rs. 4.20
Per Rupee Sales tax = (Rs. 4.20)/60
Per Rupee Sales tax = Rs. 0.07
Sales tax on the purchase worth Rs. 150 = Rs. 0.07 × 150
Sales tax on the purchase worth Rs. 150 = Rs 10.50
Thus, the sales tax on the purchase worth Rs. 150 is Rs 10.50.
Question 11: The cost of 17 chairs is Rs. 19210. Find the number of such chairs that can be purchased in Rs 113000?
Solution 11:
Chairs purchased in Rs. 19,210 is = 17
Chairs purchased in Re. 1 = 17/19,210
Chairs can be purchased in Rs. 1,13,000 = 17/19,210×1,13,000
Chairs can be purchased in Rs. 1,13,000 = 100
Therefore, In Rs. 1,13,000 100 chairs can be purchased.
Question 12: A car travels 165 km in 3 hours
(i) How long will it take to travel 440 km?
(ii) How far will it travel in 7 hours?
Solution 12:
Distance travelled by car = 165 km in 3 hours
Speed of car = Distance/Time
Speed of car = 165/3
Speed of car = 55 km/hour
(i) Time taken to travel 440 km = 440/55
Time taken to travel 440 km = 8 hours
(ii) Distance covered in 7 hours = 55 × 7
Distance covered in 7 hours = 385km
Question 13: 2 dozens of oranges cost Rs 60. Find the cost of 120 similar oranges?
Solution 13:
We know that 1 Dozens = 12 units
Cost of 2 dozens of oranges = Rs. 60
Cost of an orange = Rs. 60/24
Cost of an orange = Rs. 2.5
Cost of 120 oranges = Rs. 2.5 × 120
Cost of 120 oranges = Rs. 300
Thus, the cost of 120 such oranges is Rs 300.
Question 14: A family of 4 members consumes 6 kg of sugar in a month. What will be the monthly consumption of sugar, if the number of family members becomes 6?
Solution 14:
Sugar used by a 4 members of family = 6 kg
Sugar used by 1 member = 6/4 kg
Sugar used by 1 member = 1.5 kg
Sugar used by 6 members of a family = 1.5 × 6
Sugar used by 6 members of a family = 9 kg
Thus, Sugar used by 6 members of a family is 9 kg
Question 15: The weight of 45 folding chairs is 18 kg. How many such chairs can be loaded on a truck having a capacity of carrying 4000 kg load?
Solution 15:
The weight of 45 chairs = 18 Kg.
The weight of 1 chairs = 18/45 Kg.
The weight of 1 chairs = 0.4 Kg.
Number of chairs can load in track weighing 4000 kg = (4000 Kg.)/0.4
Number of chairs can load in track weighing 4000 kg = 10,000
Thus, 10000 chairs can be loaded on a truck having a capacity of carrying 4000 kg load.
Objective Type Questions ::->
Mark the correct alternative in each of the following:
Question 1: A ratio equivalent of 2 : 3 is
(a) 4 : 3
(b) 2 : 6
(c) 6 : 9
(d) 10 : 9
Solution 1: (c)
6 : 9
We can write it as 6/9
Change in standard form we get,
By taking HCF of numerator and denominator
(6÷3)/(9÷3)= 2/3
Hence, the equivalent ratio of 2 : 3 is 6 : 9.
Question 2: The angles of a triangle are in the ratio 1 : 2 : 3. The measure of the largest angle is
(a) 30°
(b) 60°
(c) 90°
(d) 120°
Solution 2: (c)
The sum of all angles in triangle = 180°
The largest angle = 3/6 × 180
Largest angle = 90°
Question 3: The sides of a triangle are in the ratio 2 : 3 : 5. If its perimeter is 100 cm, the length of its smallest side is
(a) 2 cm
(b) 20 cm
(c) 3 cm
(d) 5 cm
Solution 3: (b)
The length of smallest side = 100 × 2/10
The length of smallest side = 200/10
The length of smallest side = 20 cm
Question 4: Two numbers are in the ratio 7 : 9. If the sum of the numbers is 112, then the larger number is
(a) 63
(b) 42
(c) 49
(d) 72
Solution 4: (a)
Let x the largest number
7x+9x=112
16x = 112
x = 112/16
x=7
7× x = 7 × 7 = 49
9× x = 9 × 7 = 63
Thus, the largest number is 63.
Question 5: Two ratio 384 : 480 in its simplest form is
(a) 3 : 5
(b) 5 : 4
(c) 4 : 5
(d) 2 : 5
Solution 5: (c)
384 : 480
384/480 = 4/5
Question 6: If A, B, C, divide Rs 1200 in the ratio 2 : 3 : 5, then B’s share is
(a) Rs 240
(b) Rs 600
(c) Rs 380
(d) Rs 360
Solution 6: (d)
B’s share = 3/10×1200
B’s share = 3 × 120
B’s share = Rs. 360
Question 7: If a bus travels 126 km in 3 hours and a train travels 315 km in 5 hours, then the ratio of their speeds is
(a) 2 : 5
(b) 2 : 3
(c) 5 : 2
(d) 25 : 6
Solution 7: (b)
Speed = Distance/Time
Speed of bus = 126/3
Speed of bus = 42 km/h
Speed of train = 315/5
Speed of train = 63 km/h
Ratio of their speeds = 42 : 63
Ratio of their speeds = 2 : 3
Question 8: The ratio of male and female employees in a multinational company is 5 : 3. If there are 115 male employees in the company, then the number of female employees is
(a) 96
(b) 52
(c) 69
(d) 66
Solution 8: (c)
Let x the number of female employees
5/3 = 115/x
5×x=115×3
5x=345
x=345/5
x=69
Question 9: Length and width of a field are in the ratio 5 : 3. If the width of the field is 42 m, then its length is
(a) 50 m
(b) 70 m
(c) 80 m
(d) 100 m
Solution 9: (b)
Length and width of a field = 5: 3
Let the length is x m
Width of the filed = 42 m
5/3 = x/42
3×x = 42 × 5
3x=210
x=210/3
x=70
Question 10: If 57 : x = 51 : 85, then the value of x is
(a) 95
(b) 76
(c) 114
(d) None of these
Solution 10: (a)
57/x= 51/85
57 × 85 =51 ×x
4845=51x
4845/51=x
x = 95
Question 11: The ratio of boys and girls in a school is 12 : 5. If there are 840 girls in the school, then the number of boys is
(a) 1190
(b) 2380
(c) 2856
(d) 2142
Solution 11: not correct.
Let x the number of boys
Ratio of boys and girls = 12 : 5
12/5 = x/840
12×840=5×x
10,080=5x
10,080/5=x
10,080/5=x
2016=x
Question 12: If 4, a, a, 36 are in proportion, then a =
(a) 24
(b) 12
(c) 3
(d) 24
Solution 12: (b)
The proportion is 4 : a :: a : 36
4/a = a/36
4 × 36 = a × a
a2 = 144
a = 12
Question 13: If 5 : 4 : : 30 : x, then the value of x is
(a) 24
(b) 12
(c) 3/2
(d) 6
Solution 13: (a)
5/4 = 30/x
5×x=30×4
5x=120
x=120/5
x=24
Question 14: If a, b, c, d are in proportion, then
(a) ab = cd
(b) ac = bd
(c) ad = bc
(d) None of these
Solution 14: (c)
The proportion a : b :: c : d
a/b = c/d
ad = bc
Question 15: If a, b, c, are in proportion, then
(a) a2 = bc
(b) b2 = ac
(c) c2 = ab
(d) None of these
Solution 15: (b)
The proportion is a : b :: b : c
a/b = b/c
b2 = ac
Question 16: If the cost of 5 bars of a soap is Rs. 30, then the cost of one dozen bars is
(a) Rs. 60
(b) Rs. 120
(c) Rs. 72
(d) Rs. 140
Solution 16: (c)
Let Rs. x is the cost of one dozen bars
30/5 = x/12
5×x=30×12
5x=360
x= (Rs. 360)/5
x= Rs.72
Question 17: 12 men can finish a piece of work in 25 days. The number of days in which the same piece of work can be done by 20 men, is
(a) 10 days
(b) 12 days
(c) 15 days
(d) 14 days
Solution 17: (c)
Let x days required do the same work
20/12 = 25/x
20x=300
x = 300/20
x=15 days
Question 18: If the cost of 25 packets of 12 pencils each is Rs 750, then the cost of 30 packets of 8 pencils each is
(a) Rs. 600
(b) Rs. 720
(c) Rs. 640
(d) None of these
Solution 18: (a)
Cost of 300 pencils = Rs. 750
Let Rs. x the cost of 240 pencils
750 : 300 :: x : 240
750/300= x/240
750×240=x×300
1,80,000=300x
1,80,000/300=x
Thus, the Cost of 240 pencils is Rs. 600
Question 19: If a, b, c are in proportion, then
(a) a : b : : b : c
(b) a : b : : c : a
(c) a : b : : c : b
(d) a : c : : b : c
Solution 19: (a)
The proportion a: b :: b: c
a/b=b/c
ac=b2
Question 20: The first, second and fourth terms of a proportion are 16, 24 and 54 respectively. The third term is
(a) 32
(b) 48
(c) 28
(d) 36
Solution 20: (d)
Let x the third term is
16 : 24 = x : 54
16/24 = x/54
24x=16×54
x=36

