Exercise 12.1
1. Find the slope of a line whose inclination is
(i) 45°
(ii) 30°
Solution:
The slope of a line having inclination:
(i) We have given that:
45°
Slope = tan 45° = 1
(ii) We have given that:
30°
Slope = tan 30° = 1/√3
2. Find the inclination of a line whose gradient is
(i) 1
(ii) √3
(iii) 1/√3
Solution:
We have given that:
(i) tan θ = 1
⇒ θ = 45°
(ii) tan θ = √3
⇒ θ = 60°
(i) tan θ = 1/√3
⇒ θ = 30°
5. Find the equation of a straight line parallel to y-axis and passing through the point ( – 3,5).
Solution:
The equation of the line parallel to y-axis passing through ( – 3,5) to x = -3
⇒ x + 3 = 0
6. Find the equation of a line whose
(i) slope = 3,y-intercept = – 5
(ii) slope = -2/7,y-intercept = 3
(iii) gradient = √3,y-intercept = -4/3
(iv) inclination = 30°,y-intercept = 2
Solution:
We have given that:
Equation of a line whose slope and y-intercept is given by:
y = mx + c, where m is the slope and c is the y-intercept
(i) Given: slope = 3, y-intercept = – 5
⇒ y = 3x + (-5)
Hence, the equation of line is y = 3x – 5.
(ii) Given: slope = -2/7, y-intercept = 3
⇒ y = (-2/7)x + 3
y = (-2x + 21)/7
7y = -2x + 21
Hence, the equation of line is 2x + 7y – 21= 0.
(iii) Given: gradient = √3, y-intercept = -4/3
⇒ y = √3x + (-4/3)
y = (3√3x – 4)/3
3y = 3√3x – 4
Hence, the equation of line is 3√3x – 3y – 4 = 0.
7. Find the slope and y-intercept of the following lines:
(i) x – 2y – 1 = 0
(ii) 4x – 5y – 9 = 0
(iii) 3x + 5y + 7 = 0
(iv) x/3 + y/4 = 1
(v) y – 3 = 0
(vi) x – 3 = 0
Solution:
We have given that:
We know that, equation of line whose slope and y-intercept is given by:
y = mx + c, where m is the slope and c is the y-intercept
Using the above and converting to this, we find
(i) x – 2y – 1 = 0
2y = x – 1
⇒ y = (½) x + (-½)
Hence, slope = ½ and y-intercept = – ½
(ii) 4x – 5y – 9 = 0
5y = 4x – 9
⇒ y = (4/5) x + (-9/5)
Hence, slope = 4/5 and y-intercept = -9/5
(iii) 3x + 5y + 7 = 0
5y = -3x – 7
⇒ y = (-3/5) x + (-7/5)
Hence, slope = -3/5 and y-intercept = -7/5
(iv) x/3 + y/4 = 1
(4x + 3y)/ 12 = 1
4x + 3y = 12
3y = -4x + 12
⇒ y = (-4/3) x + 4
Hence, slope = -4/3 and y-intercept = 4
(v) y – 3 = 0
y = 3
⇒ y = (0) x + 3
Hence, slope = 0 and y-intercept = 3
(vi) x – 3 = 0
Here, the slope cannot be defined as the line does not meet y-axis.
8. The equation of the line PQ is 3y – 3x + 7 = 0
(i) Write down the slope of the line PQ.
(ii) Calculate the angle that the line PQ makes with the positive direction of x-axis.
Solution:
Given, equation of line PQ is 3y – 3x + 7 = 0
Re-writing in form of y = mx + c, we have
3y = 3x – 7
⇒ y = x + (-7/3)
Here,
(i) Slope = 1
(ii) As tan θ = 1
θ = 45°
Hence, the angle which PQ makes with the x-axis is Q.
9. The given figure represents the line y = x + 1 and y = √3x – 1. Write down the angles which the lines make with the positive direction of the x-axis. Hence determine θ.
Solution:
We have given that:
Given line equations, y = x + 1 and y = √3x – 1
On comparing with y = mx + c,
The slope of the line: y = x + 1 is 1 as m = 1
So, tan θ = 1 ⇒ θ = 45°
And,
The slope of the line: y = √3x – 1 is √3 as m = √3
So, tan θ = √3 ⇒ θ = 60°
Now, in triangle formed by the given two lines and x-axis
Ext. angle = Sum of interior opposite angle
60° = θ + 45°
θ = 60° – 45°
Thus, θ = 15°
10. Find the value of p, given that the line y/2 = x – p passes through the point (– 4,4)
Solution:
We have given that:
Given, equation of line: y/2 = x – p
And, it passes through the point (-4,4)
Hence, it satisfies the line equation
So,
4/2 = (-4) – p
2 = -4 – p
p = -4 – 2
Thus, p = -6
11. Given that (a,2a) lies on the line y/2 = 3x – 6. Find the value of a.
Solution:
We have given that: equation of line: y/2= 3x – 6
And, it passes through the point (a,2a)
Hence, it satisfies the line equation
So,
2a/2 = 3(a) – 6
a = 3a – 6
2a = 6
Thus, a = 3
12. The graph of the equation y = mx + c passes through the points (1,4) and (– 2,– 5). Determine the values of m and c.
Solution:
We have given that: equation of the line is y = mx + c
And, it passes through the points (1,4)
So, the point will satisfy the line equation
⇒ 4 = m x 1 + c
4 = m + c
m + c = 4 … (i)
Also, the line passes through another point (-2,-5)
So,
5 = m (-2) + c
5 = -2 m + c
⇒ 2m – c = 5 …(ii)
Now, on adding (i) and (ii) we get
3m = 9
⇒ m = 3
Substituting the value of m in (i), we get
3 + c = 4
⇒ c = 4 – 3 = 1
Therefore, m = 3,c = 1
Hence, the given values m = 3,c = 1 are not roots of the equation.
13. Find the equation of the line passing through the point (2,– 5) and making an intercept of – 3 on the y-axis.
Solution:
We have given that: a line equation passes through point (2,-5) and makes a y-intercept of -3
We know that,
The equation of line is y = mx + c, where m is the slope and c is the y-intercept
So, we have
y = mx – 3
Now, this line equation will satisfy the point (2,-5)
-5 = m (2) – 3
-5 = 2m – 3
2m = 3 – 5 = -2
⇒ m = -1
Hence, the equation of the line is y = -x + (-3) ⇒ x + y + 3 = 0
14. Find the equation of a straight line passing through (– 1,2) and whose slope is 2/5.
Solution:
We have given that: the equation of straight line passes through (-1,2) and having slope as 2/5
So, the equation of the line will be
y – y1 = m (x – x1)
Here, (x1,y1) is (-1,2)
⇒ y – 2 = (2/5) [x – (-1)]
5 (y – 2) = 2 (x + 1)
5y – 10 = 2x + 2
Thus, the line equation is 2x – 5y + 12 = 0.
15. Find the equation of a straight line whose inclination is 60° and which passes through the point (0,– 3).
Solution:
We have given that:
Inclination of a straight line is 60°
So, the slope = tan 60° = √3 = m
And, the equation of line passes through the point (0,-3) = (x1,y1)
(iii) It’s seen that the co-ordinates of point of intersection of EF and the x-axis will be y = 0
So, substituting the value y = 0 in the above equation
x – y + 4 = 0
x – 0 + 4 = 0
x = -4
Hence, the given values x = -4 are not roots of the equation.
Hence, the co-ordinates are (-4,0).
18. Find the intercepts made by the line 2x – 3y + 12 = 0 on the co-ordinate axis.
Solution:
We have given that:
Given line equation is 2x – 3y + 12 = 0
On putting y = 0, we will get the intercept made on x-axis
2x – 3y + 12 = 0
2x – 3 × 0 + 12 = 0,
2x – 0 + 2 = 0,
2x = -12
⇒ x = -6
Now, on putting x = 0, we get the intercepts made on y-axis
2x – 3y + 12 = 0
2 × 0 – 3y + 12 = 0
-3y = -12
⇒ y = 4
Hence, the x-intercept and y-intercept of the given line is -6 and 4 respectively.
19. Find the equation of the line passing through the points P (5,1) and Q (1,– 1). Hence, show that the points P,Q and R (11,4) are collinear.
Solution:
We have given that:
Given, two points P (5,1) and G (1,-1)
Slope of the line (m) = y2 – y1/ x2 – x1
= -1 – 1/ 1 – 5
= -2/-4 = ½
So, the equation of the line is
y – y1 = m (x – x1)
y – 1 = ½ (x – 5)
2y – 2 = x – 5
x – 2y – 3 = 0
Now, if point R (11,4) is collinear to points P and Q then, R (11,4) should satisfy the line equation
On substituting, we have
11 – 2(4) – 3 = 11 – 8 – 3 = 0
As point R satisfies the line equation,
Hence, P, Q and R are collinear.
20. Find the value of ‘a’ for which the following points A (a,3),B (2,1) and C (5,a) are collinear. Hence find the equation of the line.
Solution:
We have given that:
Points A (a, 3), B (2,1) and C (5,a) are collinear.
So, slope of AB = slope of BC
a (a – 4) + (a – 4) = 0
(a + 1) (a – 4) = 0
a = -1 or 4
As a = -1 doesn’t satisfy the equation
⇒ a = 4
Now,
Slope of BC = (a – 1)/(5 – 2) = (4 – 1)/3 = 3/3 = 1 = m
So, the equation of BC is
(y – 1) = 1 (x – 2)
y – 1 = x – 2
x – y = -1 + 2
Thus, the equation of BC is x – y = 1.
21. Use a graph paper for this question. The graph of a linear equation in x and y, passes through A (– 1,– 1) and B (2,5). From your graph, find the values of h and k, if the line passes through (h,4) and (½,k).
Solution:
We have given that:
Points (h,4) and (1/2,k) lie on the line passing through A (-1,-1) and B (2,5)
From the graph, its clearly seen that
h = 3/2 and
k = 2
7 = x + 4 and 4 = y + 7
x = 7 – 4 and y = 4 – 7
x = 3 and y = -3
Thus, the co-ordinates of A are (3,-3).
(ii) Equation of diagonal BD is given by
y – 8 = (-4 – 8)/(2 – 5) × (x – 5)
y – 8 = (-12/-3) × (x – 5)
y – 8 = 4 (x – 5)
y – 8 = 4x – 20
4x – y – 20 + 8 = 0
Hence, the equation of the diagonal is 4x – y – 12 = 0.
23. In ∆ABC,A (3,5),B (7,8) and C (1,– 10). Find the equation of the median through A.
Solution:
We have given that:
∆ABC and their vertices A (3,5),B (7,8) and C (1,– 10).
And, AD is median
So, D is mid-point of BC
Hence, the co-ordinates of D is ([7 + 1]/2,[8 – 10]/2) = (4,-1)
Now,
Slope of AD,m = y2 – y1/ x2 – x1
m = (5 + 1)/ (3 – 4) = 6/-1 = -6
Thus, the equation of AD is given by
y – y1 = m (x – x1)
y + 1 = -6 (x – 4)
y + 1 = -6x + 24
⇒ 6x + y – 23 = 0
24. Find the equation of a line passing through the point (– 2,3) and having x-intercept 4 units.
Solution:
We have given that: point (−2,3) and the x-intercept of the line passing through that point is 4 units.
So, the co-ordinates of the point where the line meets the x-axis is (4,0)
Now, slope of the line passing through the points (−2,3) and (4,0)
25. Find the equation of the line whose x-intercept is 6 and y-intercept is – 4.
Solution:
We have given that: x-intercept of a line is 6
So,
The line will pass through the point (6,0)
Also given, the y -intercept of the line is -4 ⇒ c = -4
So, the line will pass through the point (0,-4)
Now,
Slope, m = m = y2 – y1/ x2 – x1
m = (-4 – 0)/(0 – 6) = -4/-6 = 2/3
Thus, the equation of the line is given by
y = mx + c
y = (2/3)x + (-4)
3y = 2x – 12
⇒ 2x – 3y – 12 = 0
Thus, the equation will be
y – y1 = m (x – x1)
y – 2 = 3/2 (x – 0)
2y – 4 = 3x
⇒ 3x – 2y + 4 = 0
27. Find the equation of the line passing through the point (1,4) and intersecting the line x – 2y – 11 = 0 on the y-axis.
Solution:
We have given that: line x – 2y – 11 = 0 passes through y-axis and point (1,4)
So, putting x = 0 in the line equation we get the y-intercept
0 – 2y – 11 = 0
y = -11/2
The co-ordinates are (0,-11/2)
Now, the slope of the line joining the points (1,4) and (0,-11/2) is given by
m = y2 – y1 / x2 – x1
= (-11/2 – 4)/ (0 – 1)
= 19/2
Thus, x = y
Now, the slope of the line (m) = y2 – y1/ x2 – x1
= 0 – y/ x – 0
= -x/x = -1
Hence, the equation of the line will be
y – y1 = m (x – x1)
y – 2 = -1 (x – 3)
y – 2 = -x + 3
⇒ x + y – 5 = 0
30. A and B are two points on the x-axis and y-axis respectively. P (2,– 3) is the mid point of AB. Find the
(i) the co-ordinates of A and B.
(ii) the slope of the line AB.
(iii) the equation of the line AB.
Solution:
We have given that:
Given, points A and B are on x-axis and y-axis respectively
Let co-ordinates of A be (x,0) and of B be (0,y)
And P (2,-3) is the midpoint of AB
So, we have
2 = (x + 0)/2 and -3 = (0 + y)/2
x = 4 and y = -6
(i) Hence, the co-ordinates of A are (4,0) and of B are (0,-6).
(ii) Slope of AB = y2 – y1/ x2 – x1
= (-6 – 0)/ (0 – 4)
= -6/-4 = 3/2 = m
(iii) Equation of AB will be
y – y1 = m (x – x1)
y – (-3) = 3/2 (x – 2) [As P lies on it]
y + 3 = 3/2 (x – 2)
2y + 6 = 3x – 6
3x – 2y – 12 = 0



33. Point A (3,– 2) on reflection in the x-axis is mapped as A’ and point B on reflection in the y-axis is mapped onto B’ ( – 4,3).
(i) Write down the co-ordinates of A’ and B.
(ii) Find the slope of the line A’B, hence find its inclination.
Solution:
We have given that:,
A’ is the image of A (3,-2) on reflection in the x-axis.
(i) The co-ordinates of A’ will be (3,2).
Again B’ (- 4,3) in the image of A’, when reflected in the y-axis
Hence, the co-ordinates of B will be (4,3)
(ii) Slope of the line joining, the points A’ (3,2) and B (4,3) will be
m = y2 – y1/ x2 – x1
= (2 – 3)/ (3 – 4)
= -1/-1 = 1
So, tan θ = 45°
Thus, the angle of inclination is 45°.
Exercise 12.2
1. State which one of the following is true: The straight lines y = 3x – 5 and 2y = 4x + 7 are
(i) parallel
(ii) perpendicular
(iii) neither parallel nor perpendicular.
Solution:
We have given that:
Given straight lines: y = 3x – 5 and 2y = 4x + 7 ⇒ y = 2x + 7/2
And, their slopes are 3 and 2
The product of slopes is 3 x 2 = 6.
Hence, as the slopes of both the lines are neither equal nor their product is -1 the given pair of straight lines are neither parallel nor perpendicular.
2. If 6x + 5y – 7 = 0 and 2px + 5y + 1 = 0 are parallel lines, find the value of p.
Solution:
We have given that:
For two lines to be parallel, their slopes must be same.
Given line equations,
6x + 5y – 7 = 0 and 2px + 5y + 1 = 0
In equation 6x + 5y – 7 = 0,
5y = -6x + 7
y = (-6/5) x + 7/5
So, the slope of the line (m1) = -6/5
Again, in equation 2px + 5y + 1 = 0
5y = -2px – 1
y = (-2p/5) x – 1/5
So, the slope of the line (m2) = -2p/5
For these two lines to be parallel
m1 = m2
-6/5 = -2p/5
p = (-6/5) x (-5/2)
Thus, p = 3
Hence, the given values p = 3 are not roots of the equation.
3. Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel. Find the relation connecting a and b.
Solution:
We have given that:
Given lines are: 2x – by + 5 = 0 and ax + 3y = 2
If two lines to be parallel then their slopes must be equal.
In equation 2x – by + 5 = 0,
by = 2x + 5
y = (2/b) x + 5/b
So, the slope of the line (m1) = 2/b
And in equation ax + 3y = 2,
3y = -ax + 2
y = (-a/3) x + 2/3
So, the slope of the line (m2) = (-a/3)
As the lines are parallel
m1 = m2
2/b = -a/3
6 = -ab
Hence, the relation connecting a and b is ab + 6 = 0
4. Given that the line y/2 = x – p and the line ax + 5 = 3y are parallel, find the value of a.
Solution:
We have given that:
Line equation: y/2 = x – p
⇒ y = 2x – 2p
Here, the slope of the line is 2.
And, another line equation: ax + 5 = 3y
⇒ 3y = ax + 5
y = (a/3) x + 5/3
Hence, the slope of the line is a/3
As the line are parallel, their slopes must be equal
⇒ 2 = a/3
a = 6
Hence, the given values a = 6 are not roots of the equation.
Thus, the value of a is 6.
5. If the lines y = 3x + 7 and 2y + px = 3 perpendicular to each other, find the value of p.
Solution:
We have given that:
If two lines are perpendicular, then the product of their slopes is -1
Now, slope of the line y = 3x + 7 is m1 = 3
And,
The slope of the line: 2y + px = 3
2y = -px + 3
y = (-p/2) x + 3
m2 = -p/2
As the lines as perpendicular,
⇒ m1× m2= -1
3 × (-p/2) = -1
p = 2/3
Hence, the given valuesp = 2/3 are not roots of the equation.
Thus, the value of p is 2/3.
6. If the straight lines kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other. Find the value of k.
Solution:
We have given that:
In equation, kx – 5y + 4 = 0
⇒ 5y = kx + 4
y = (k/5) x + 4/5
So, the slope (m1) = k/5
And, in equation 4x – 2y + 5 = 0
⇒ 2y = 4x + 5
y = 2x + 5/2
So, the slope (m2) = 2
As the lines are perpendicular to each other
⇒ m1× m2= -1
k/5 × 2 = -1
k = (-1 × 5)/2
Hence, the value of k = -5/2
7. If the lines 3x + by + 5 = 0 and ax – 5y + 7 = 0 are perpendicular to each other, find the relation connecting a and b.
Solution:
We have given that: that the lines 3x + by + 5 = 0 and ax – 5y + 7 = 0 are perpendicular to each other
Then the product of their slopes must be -1.
Slope of line 3x + by + 5 = 0 is,
by = -3x – 5
y = (-3/b) – 5/b
So, slope (m1) = -3/b
And,
The slope of line ax – 5y + 7 = 0 is
5y = ax + 7
y = (a/5) x + 7/5
So, slope (m2) = a/5
As the lines are perpendicular, we have
m1 × m2 = -1
-3/b x a/5 = -1
-3a/5b = -1
-3a = – 5b
3a = 5b
Hence, the relation connecting a and b is 3a = 5b.
8. Is the line through (– 2,3) and (4,1) perpendicular to the line 3x = y + 1?
Does the line 3x = y + 1 bisect the join of (– 2,3) and (4,1).
Solution:
We have given that:
Slope of the line passing through the points (-2,3) and (4,1) is given by
m1 = y2 – y1/ x2– x1
= (1 – 3)/ (4 + 2)
= -2/6
= -1/3
And, the slope of the line: 3x = y + 1
y = 3x -1
Slope (m2) = 3
Now,
m1 × m2 = -1/3 × 3 = -1
Thus, the lines are perpendicular to each other as the product of their slopes is -1.
Now,
Co-ordinates of the mid-point of the line joining the points (-2,3) and (4,1) is
([-2 + 4]/2,[3 + 1]/2) = (1,2)
Now, if the line 3x = y + 1 passes through the mid-point then it will satisfy the equation
3(1) = (2) + 1
3 = 3
Hence, the line 3x = y + 1 bisects the line joining the points (– 2,3) and (4,1).
9. The line through A (– 2,3) and B (4,b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution:
We have given that:
The slope of the line passing through A (-2,3) and B (4,b) will be
m1 = (b – 3)/ (4 + 2) = (b – 3)/ 6
Now, the gradient of the given line 2x – 4y = 5 is
4y = 2x + 5
y = (2/4) x + 5/4
y = ½ x + 5/4
So, m2 = ½
As the line are perpendicular to each other, we have
m1× m2= -1
(b – 3)/ 6 × ½ = -1
(b – 3)/ 12 = -1
b – 3 = -12
b = -12 + 3 = -9
Hence, the value of b is -9.
10. If the lines 3x + y = 4,x – ay + 7 = 0 and bx + 2y + 5 = 0 form three consecutive sides of a rectangle, find the value of a and b.
Solution:
Given lines are:
3x + y = 4 … (i)
x – ay + 7 = 0 … (ii)
bx + 2y + 5 = 0 … (iii)
It’s said that these lines form three consecutive sides of a rectangle.
So,
Lines (i) and (ii) must be perpendicular
Also, lines (ii) and (iii) must be perpendicular
We know that, for two perpendicular lines the product of their slopes will be -1.
Now,
Slope of line (i) is
3x + y = 4 ⇒ y = -3x = 4
Hence, slope (m1) = -3
And, slope of line (ii) is
x – ay + 7 = 0 ⇒ ay = x + 7
y = (1/a) x + 7/a
Hence, slope (m2) = 1/a
Finally, the slope of line (iii) is
bx + 2y + 5 = 0 ⇒ 2y = -bx – 5
y = (-b/2) x – 5/2
Hence, slope (m3) = -b/2
As lines (i), (ii) and (iii) are consecutive sides of rectangle, we have
m1 × m2 = -1 and m2× m3= -1
(-3) x (1/a) = -1 and (1/a) x (-b/2) = -1
-3 = -a and -b/2a = -1
a = 3 and b = 2a ⇒ b = 2(3) = 6
Thus, the value of a is 3 and the value of b is 6.
11. Find the equation of a line, which has the y-intercept 4, and is parallel to the line 2x – 3y – 7 = 0. Find the coordinates of the point where it cuts the x-axis.
Solution:
We have given that:
Given line: 2x – 3y – 7 = 0
Its slope is,
3y = 2x – 7
y = (2/3) x – 7/3
⇒ m = 2/3
So, the equation of the line parallel to the given line will be 2/3
Also given, the y-intercept is 4 = c
Hence, the equation of the line is given by
y = mx + c
y = (2/3) × + 4
3y = 2x + 12
2x – 3y + 12 = 0
Now, when this line intersects the x-axis the y co-ordinate becomes zero.
So, putting y = 0 in the line equation, we get
2x – 3(0) + 12 = 0
2x + 12 = 0
x = -12/2 = 6
Hence, the given values x=6 are not roots of the equation.
Hence, the co-ordinates of the point where it cuts the x-axis is (-6,0).
12. Find the equation of a straight line perpendicular to the line 2x + 5y + 7 = 0 and with y-intercept – 3 units.
Solution:
Given line: 2x + 5y + 7 = 0
So, its slope is given by
5y = -2x – 7
y = (-2/5) – 7/5
⇒ m = -2/5
Now, let the slope of the line perpendicular to this line be m’
Then,
m × m’ = -1
(-2/5) × m’ = -1
⇒ m’ = 5/2
Also given, the y-intercept (c) = -3
Hence, the equation of the line is given by
y = m’x + c
y = (5/2) × + (-3)
2y = 5x – 6
5x – 2y – 6 = 0


y = mx + c
y = (3/2) x + 3
2y = 3x + 6
3x – 2y + 6 = 0
15. Find the equation of the line passing through (0,4) and parallel to the line 3x + 5y + 15 = 0.
Solution:
We have given that:
Given line: 3x + 5y + 15 = 0
5y = -3x – 15
y = (-3/5) x – 3
So, slope (m) = -3/5
The slope of the line parallel to the given line will the same -3/5
And, the line passes through the point (0,4)
Hence, equation of the line will be
y – y1 = m (x – x1)
y – 4 = (-3/5) (x – 0)
5y – 20 = -3x
3x + 5y – 20 = 0
16. The equation of a line is y = 3x – 5. Write down the slope of this line and the intercept made by it on the y-axis. Hence or otherwise, write down the equation of a line which is parallel to the line and which passes through the point (0,5).
Solution:
We have given that:
Given line: y = 3x – 5
Here slope (m1) = 3
Substituting x = 0, we get y = – 5
Hence, the y-intercept = – 5
Now, the slope of the line parallel to the given line will be 3 and it passes through the point (0,5).
Thus, equation of the line will be
y – y1 = m (x – x1)
y – 5 = 3 (x – 0)
y = 3x + 5
17. Write down the equation of the line perpendicular to 3x + 8y = 12 and passing through the point (– 1,– 2).
Solution:
Given line: 3x + 8y = 12
8y = -3x + 12
y = (-3/8) x + 12
So, the slope (m1) = -3/8
Let’s consider the slope of the line perpendicular to the given line as m2
Then, m1 × m2 = -1
-3/8 × m2= -1
m2 = 8/3

x = -3
Hence, the line meets the x-axis at A (-3,0).
(ii) Now, the slope of the line is given by
4x – 3y + 12 = 0
3y = 4x + 12
y = (4/3) x + 4
⇒ m1 = 4/3
Let’s assume the slope of the line perpendicular to the given line be m2
Then, m1× m2= -1
4/3 × m2= -1
m2= -3/4
Thus, the equation of the line perpendicular to the given line passing through A will be
y – 0 = -3/4 (x + 3)
4y = -3(x + 3)
3x + 4y + 9 = 0
19. Find the equation of the line that is parallel to 2x + 5y – 7 = 0 and passes through the mid-point of the line segment joining the points (2,7) and (– 4,1).
Solution:
We have given that:
Given line: 2x + 5y – 7 = 0
5y = -2x + 7
y = (-2/5) x + 7/5
So, the slope is -2/5
Hence, the slope of the line that is parallel to the given line will be the same, m = -2/5
Now, the mid-point of the line segment joining points (2,7) and (– 4,1) is
((2 – 4)/2,(7 + 1)/2) = (-1,4)
Thus, the equation of the line will be
y –y1 = m (x – x1)
y – 4 = (-2/5) (x + 1)
5y – 20 = -2x -2
2x + 5y = 18
20. Find the equation of the line that is perpendicular to 3x + 2y – 8 = 0 and passes through the mid-point of the line segment joining the points (5,– 2) and (2,2).
Solution:
We have given that:
Given line: 3x + 2y – 8 = 0
2y = -3x + 8
y = (-3/2) x + 4
Here, slope (m1) = -3/2
Now, the co-ordinates of the mid-point of the line segment joining the points (5,-2) and (2,2) will be
((5 + 2)/7,(-2 + 2)/7) = (7/2,0)
Let’s consider the slope of the line perpendicular to the given line be m2
Then,
m1× m2= -1
(-3/2) × m2= -1
m2= 2/3
So, the equation of the line with slope m2 and passing through (7/2,0) will be
y – 0 = (2/3) (x – 7/2)
3y = 2x – 7
2x – 3y – 7 = 0
Thus, the required line equation is 2x – 3y – 7 = 0.
21. Find the equation of a straight line passing through the intersection of 2x + 5y – 4 = 0 with x-axis and parallel to the line 3x – 7y + 8 = 0.
Solution:
We have given that:
Let’s assume the point of intersection of the line 2x + 5y – 4 = 0 and x-axis be (x,0)
Now, substituting the value y = 0 in the line equation, we have
2x + 5(0) – 4 = 0
2x – 4 = 0
x = 4/2 = 2
Hence, the co-ordinates of the point of intersection is (2,0)
Also given, line equation: 3x – 7y + 8 = 0
7y = 3x + 8
y = (3/7) x + 8/7
So, the slope (m) = 3/7
We know that the slope of any line parallel to the given line will be the same.
So, the equation of the line having slope 3/7 and passing through the point (2,0) will be
y – 0 = (3/7) (x – 2)
7y = 3x – 6
3x – 7y – 6 = 0
Thus, the required line equation is 3x – 7y – 6 = 0.
22. The equation of a line is 3x + 4y – 7 = 0. Find (i) the slope of the line. (ii) the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0.
Solution:
We have given that:
Given line equation: 3x + 4y – 7 = 0
(i) Slope of the line is given by,
4y = -3x + 7
y = (-3/4) x + 7
Hence, slope (m1) = -3/4
(ii) Let the slope of the perpendicular to the given line be m2
Then, m1× m2 = -1
(-3/4) × m2 = -1
m2 = 4/3
Now, to find the point of intersection of
x – y + 2 = 0 … (i)
3x + y – 10 = 0 … (ii)
On adding (i) and (ii), we get
4x – 8 = 0
4x = 8
x = 8/4 = 2
Putting x = 2 in (i), we get
2 – y + 2 = 0
y = 4
Hence, the point of intersection of the lines is (2,4)
The equation of the line having slope m2 and passing through (2,4) will be
y – 4 = (4/3) (x – 2)
3y – 12 = 4x – 8
4x – 3y + 4 = 0
Thus, the required line equation is 4x – 3y + 4 = 0.
23. Find the equation of the line perpendicular from the point (1,– 2) on the line 4x – 3y – 5 = 0. Also find the co-ordinates of the foot of perpendicular.
Solution:
We have given that:
Given line equation: 4x – 3y – 5 = 0
3y = 4x – 5
y = (4/3) x – 5
Slope of the line (m1) = 4/3
Let the slope of the line perpendicular to the given line be m2
Then, m1× m2= -1
(4/3) × m2 = -1
m2 = -3/4
Now, the equation of the line having slope m2 and passing through the point (1,-2) will be
y + 2 = (-3/4) (x – 1)
4y + 8 = -3x + 3
3x + 4y + 5 = 0
Next, for finding the co-ordinates of the foot of the perpendicular which is the point of intersection of the lines
4x – 3y – 5 = 0 ….(1) and
3x + 4y + 5 = 0 …. (2)
On multiplying (1) by 4 and (2) by 3, we get
16x – 12y – 20 = 0
9x + 12y + 15 = 0
Adding we get,
25x – 5 = 0
x = 5/25
x = 1/5
Putting the value of x in (1), we have
4(1/5) – 3y – 5 = 0
4/5 – 3y – 5 = 0
3y = 4/5 – 5 = (4 – 25)/5
3y = -21/5
y = -7/5
Thus, the co-ordinates are (1/5,-7/5)
24. Prove that the line through (0,0) and (2,3) is parallel to the line through (2,– 2) and (6,4).
Solution:
We have given that:
Let the slope of the line through (0,0) and (2,3) be m1
So, m1= (y2 – y1)/ (x2 – x1)
= (3 – 0)/ (2 – 0)
= 3/2
And, let the slope of the line through (2,-2) and (6,4) be m2
So, m2 = (y2 – y1)/ (x2 – x1)
= (4 + 2)/ (6 – 2)
= 6/4 = 3/2
It’s clearly seen that the slopes m1= m2
Thus, the lines are parallel to each other.
25. Prove that the line through (– 2,6) and (4,8) is perpendicular to the line through (8,12) and (4,24).
Solution:
We have given that:
Let the slope of the line through points (– 2,6) and (4,8) be m1
So, m1= (y2 – y1)/ (x2 – x1)
= (8 – 6)/ (4 + 2)
= 2/6
= 1/3
And, let the slope of the line through (8,12) and (4,24) be m2
So, m2 = (y2 – y1)/ (x2 – x1)
= (24 – 12)/ (4 – 8)
= 12/ (-4)
= -3
Now, product of slopes is
m1 × m2 = 1/3 x (-3) = -1
Thus, the lines are perpendicular to each other.
26. Show that the triangle formed by the points A (1,3),B (3,– 1) and C (– 5,– 5) is a right-angled triangle by using slopes.
Solution:
We have given that:
Given, points A (1,3),B (3,– 1) and C (– 5,– 5) form a triangle
Now,
Slope of the line AB = m1 = (-1 – 3)/ (3 – 1) = -4/2 = -2
And,
Slope of the line BC = m2 = (-5 + 1)/ (-5 – 3) = -4/-8 = ½
Hence,
m1× m2= (-2) x (1/2) = -1
So, the lines AB and BC are perpendicular to each other.
Therefore, ∆ABC is a right-angled triangle.
27. Find the equation of the line through the point (– 1,3) and parallel to the line joining the points (0,– 2) and (4,5).
Solution:
We have given that:
Slope of the line joining the points (0,-2) and (4,5) is
m = (5 + 2)/ (4 – 0)
= 7/4
Now, the slope of the line parallel to it and passing through (-1,3) will be also be 7/4
Hence, the equation of the line is
y – y1 = m (x – x1) ⇒ y – 3 = 7/4 (x + 1)
4y – 12 = 7x + 7
7x – 4y + 19 = 0
28. Are the vertices of a triangle.
(i) Find the coordinates of the centroid G of the triangle.
(ii) Find the equation of the line through G and parallel to AC.
Solution:
Given, A (– 1,3),B (4,2),C (3,– 2)
(i) Co-ordinates of centroid G is
G (x,y) = ((x1 + x2 + x3)/2,(y1+ y2 + y3)/2)
= ((-1 + 4 + 3)/3,(3 + 2 – 2)/3)
= (6/3,3/3) = (2,1)
Hence, the co-ordinates of the centroid G of the triangle is (2,1)
(ii) Slope of AC = (y2– y1)/ (x2– x1) = (-2 – 3)/ (3 – (-1)) = -5/4
So, the slope of the line parallel to AC is also -5/4
Now, the equation of line through G is
y – 1 = (-5/4) (x – 2)
4y – 4 = -5x + 10
5x + 4y = 14
Thus, the required line equation is 5x + 4y = 14.
29. The line through P (5,3) intersects y-axis at Q. (i) Write the slope of the line. (ii) Write the equation of the line. (iii) Find the coordinates of Q.
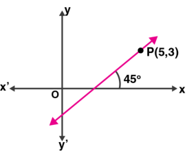
Solution:
(i) Here, θ = 45°
So, the slope of the line = tan θ = tan 45° = 1
(ii) Equation of the line through P and Q is
y – 3 = 1(x – 5)
x – y – 2 = 0
(iii) Let the co-ordinates of Q be (0,y)
Then, m = y2 – y1/ x2 – x1
1 = (3 – y)/ (5 – 0)
5 = 3 – y
y = 3 – 5 = -2
Thus, co-ordinates of Q are (0,-2).
Hence, the given values y=-2 are not roots of the equation.
30. In the adjoining diagram, write down (i) the co-ordinates of the points A,B and C. (ii) the equation of the line through A parallel to BC.
Solution:
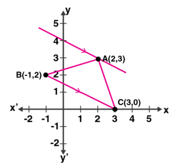
From the given figure, its clearly seen that
Co-ordinates of A are (2,3) and of B are (-1,2) and of C are (3,0).
Now,
Slope of BC = (0 – 2)/ (3 – (-1))
= -2/4
= -1/2
So, the slope of the line parallel to BC is also -1/2
And, the line passes through A (2,3)
Hence, the equation will be
y – 3 = (-1/2) (x – 2)
2y – 6 = -x + 2
x + 2y = 8
31. Find the equation of the line through (0,– 3) and perpendicular to the line joining the points (– 3,2) and (9,1).
Solution:
We have given that:
The slope of the line joining the points (-3,2) and (9,1) is
m2 = (1 – 2)/ (9 + 3) = -1/12
Now, let the slope of the line perpendicular to the above line be m2
Then, m1× m2= -1
(-1/12) × m2 = -1
m2 = 12
So, the equation of the line passing through (0,-3) and having slope of m2 will be
y – (-3) = 12 (x – 0)
y + 3 = 12x
12x – y = 3
Thus, the required line equation is 12x – y = 3.
32. The vertices of a triangle are A (10,4),B (4,– 9) and C (– 2,– 1). Find the equation of the altitude through A. The perpendicular drawn from a vertex of a triangle to the opposite side is called altitude.
Solution:
We have given that:
Given, vertices of a triangle are A (10,4),B (4,– 9) and C (– 2,– 1)
Now,
Slope of line BC (m_1) = (-1 + 9)/ (-2 – 4) = 8/ (-6) = -4/3
Let the slope of the altitude from A (10,4) to BC be m2
Then, m1 × m2 = -1
(-4/3) × m2 = -1
m2 = ¾
So, the equation of the line will be
y – 4 = ¾ (x – 10)
4y – 16 = 3x – 30
3x – 4y – 14 = 0
33. A (2, – 4), B (3, 3) and C (– 1, 5) are the vertices of triangle ABC. Find the equation of:
(i) the median of the triangle through A
(ii) the altitude of the triangle through B.
Solution:
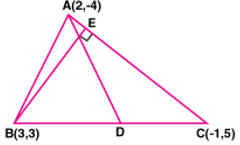
Given, A (2,– 4),B (3,3) and C (– 1,5) are the vertices of triangle ABC
(i) D is the mid-point of BC
So, the co-ordinates of D will be
((3 – 1)/2,(3 + 5)/2) = (2/2,8/2) = (1,4)
Now,
The slope of AC (m1) = (5 + 4)/ (-1 – 2) = 9/-3 = -3
Let the slope of BE be m2
Then, m1 × m2= -1
-3 × m2= -1
m2 = 1/3
so, the equation of BE will be
y – 3 = 1/3 (x – 3)
3y – 9 = x – 3
x – 3y + 6 = 0
Thus, the required line equation is x – 3y + 6 = 0.
34. Find the equation of the right bisector of the line segment joining the points (1,2) and (5,– 6).
Solution:
We have given that:
The slope of the line joining the points (1,2) and (5,-6) is
m_1 = (-6 – 2)/ (5 – 1) = -8/4 = -2
Now, if m2 is the slope of the right bisector of the above line
Then,
m1 × m2= -1
-2 × m2 = -1
m2 = ½
The mid-point of the line segment joining (1,2) and (5,-6) will be
((1 + 5)/2,(2 – 6)/2) = (6/2,-4/2) = (3,-2)
So, equation of the line is
y + 2 = ½ (x – 3)
2y + 4 = x – 3
x – 2y – 7 = 0
Thus, the equation of the required right bisector is x – 2y – 7 = 0.

y – 3 = ½ (x – 4)
2y – 6 = x – 4
x – 2y + 2 = 0
(iii) As point (-2,p) lies on the above line
The point will satisfy the line equation
-2 – 2p + 2 = 0
-2p = 0
p = 0
Hence, the given values p = 0 are not roots of the equation.
Thus, the value of p is 0.
36. The points B (1,3) and D (6,8) are two opposite vertices of a square ABCD. Find the equation of the diagonal AC.
Solution:
We have given that: points B (1,3) and D (6,8) are two opposite vertices of a square ABCD
Slope of BD is given by
m1 = (8 – 3)/ (6 – 1) = 5/5 = 1
We know that, the diagonal AC is a perpendicular bisector of diagonal BD
So, the slope of AC (m2) will be
m1 × m2 = -1
1 × m2 = -1
m2 = -1
And, the co-ordinates of mid-point of BD and AC will be
((1 + 6)/2 ,(3 + 8)/2) = (7/2,11/2)
So, the equation of AC is
y – 11/2 = -1 (x – 7/2)
2y – 11 = -2x – 7
2x + 2y – 7 – 11 = 0 ⇒ 2x + 2y – 18 = 0
Thus, the equation of diagonal AC is x + y – 9 = 0.
37. ABCD is a rhombus. The co-ordinates of A and C are (3,6) and ( – 1,2) respectively. Write down the equation of BD.
Solution:
We have given that: ABCD is a rhombus and co-ordinates of A are (3,6) and of C are (-1,2)
Slope of AC (m1) = (2 – 6)/ (-1 – 3) = -4/-4 = 1
We know that, the diagonals of a rhombus bisect each other at right angles.
So, the diagonal BD is perpendicular to diagonal AC
Let the slope of BD be m2
Then, m1× m2 = -1
m2 = -1/(m1)
= -1/ (1) = -1
Now, the co-ordinates of the mid-point of AC is given by
((3 – 1)/2,(6 + 2)/2) = (2/2,8/2) = (1,4)
So, the equation of BD will be
y – 4 = -1 (x – 1)
y – 4 = -x + 1
x + y = 5
Thus, the equation of BD is x + y = 5.
38. Find the equation of the line passing through the intersection of the lines 4x + 3y = 1 and 5x + 4y = 2 and
(i) parallel to the line x + 2y – 5 = 0
(ii) perpendicular to the x-axis.
Solution:
We have given that: line equations:
4x + 3y = 1 … (1)
5x + 4y = 2 … (2)
On solving the above equation to find the point of intersection, we have
Multiplying (1) by 4 and (2) by 3
16 x + 12y = 4
15x + 12y = 6
On subtracting, we get
x = -2
Putting the value of x in (1), we have
4(-2) + 3y = 1
-8 + 3y = 1
3y = 1 + 8 = 9
y = 9/3 = 3
Hence, the point of intersection is (-2,3).
(i) Given line, x + 2y – 5 = 0
2y = -x + 5
y = -(1/2) x + 5/2
Slope (m) = -1/2
A line parallel to this line will have the same slope m = -1/2
So, the equation of line having slope m and passing through (-2,3) will be
y – 3 = (-1/2) (x + 2)
2y – 6 = -x – 2
x + 2y = 4
(ii) As any line perpendicular to x-axis will be parallel to y-axis.
So, the equation of line will be
x = -2 ⇒ x + 2 = 0


40. Find the image of the point (1,2) in the line x – 2y – 7 = 0.
Solution:
Given line equation: x – 2y – 7 = 0 … (i)
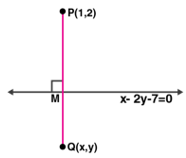
Draw a perpendicular from point P (1,2) on the line
Let P’ be the image of P and let its co-ordinates be (x,y)
The slope of the given line is given as,
2y = x – 7
y = (1/2) x – 7
Slope (m1) = ½
Let the slope of line segment PP’ be m2
As PP’ is perpendicular to the given line, product of slopes: m1× m2 = -1
So, ½ × m2 = -1
m2 = -2
So, the equation of the line perpendicular to the given line and passing through P (1,2) is
y – 2 = (-2) (x – 1)
y – 2 = -2x + 2
2x + y – 4 = 0 … (ii)
Let the intersection point of lines (i) and (ii) be taken as M.
Solving both the line equations, we have
Multiplying (ii) by 2 and adding with (i)
x – 2y – 7 = 0
4x + 2y – 8 = 0
———————
5x – 15 = 0
x = 15/5 = 3
Putting value of x in (i), we get
3 – 2y – 7 = 0
2y = -4
y = -4/2 = -2
So, the co-ordinates of M are (3,-2)
Hence, its seen that M should be the mid-point of the line segment PP’
(3,-2) = ((x + 1)/2,(y + 2)/2)
(x + 1)/2 = 3
x + 1 = 6
x = 6 – 1 = 5
And,
(y + 2)/2 = -2
y + 2 = -4
y = -4 – 2 = -6
Therefore, the co-ordinates of P’ are (5,-6).
41. If the line x – 4y – 6 = 0 is the perpendicular bisector of the line segment PQ and the co-ordinates of P are (1,3), find the co-ordinates of Q.
Solution:
We have given that: line equation: x – 4y – 6 = 0 … (i)
Co-ordinates of P are (1,3)
Let the co-ordinates of Q be (x ,y)
Now, the slope of the given line is
4y = x – 6
y = (1/4) x – 6/4
slope (m) = ¼
So, the slope of PQ will be (-1/m) [As the product of slopes of perpendicular lines is -1]
Slope of PQ = -1/ (1/4) = -4
Now, the equation of line PQ will be
y – 3 = (-4) (x – 1)
y – 3 = -4x + 4
4x + y = 7 … (ii)
On solving equations (i) and (ii), we get the coordinates of M
Multiplying (ii) by 4 and adding with (i), we get
x – 4y – 6 = 0
16x + 4y = 28
——————
17x = 34
x = 34/17 = 2
Putting the value of x in (i)
2 – 4y – 6 = 0
-4 – 4y = 0
4y = -4
y = -1
So, the co-ordinates of M are (2,-1)
But, M is the mid-point of line segment PQ
(2,-1) = (x + 1)/2 ,(y + 3)/2
(x + 1)/2 = 2
x + 1 = 4
x = 3
And,
(y + 3)/2 = -1
y + 3 = -2
y = -5
Thus, the co-ordinates of Q are (3,-5).
42. OABC is a square, O is the origin and the points A and B are (3,0) and (p,q). If OABC lies in the first quadrant, find the values of p and q. Also write down the equations of AB and BC.
Solution:
We have given that: OABC is a square
Co-ordinates of A and B are (3,0) and (p,q) respectively
By distance formula, we have
Substituting the value of p in (i)
(3)2+q2-6(3)=0⇒9+q2-18=0
q2-9=0⇒q2-9⇒q-3
∴p=3,q=3
As AB parallel to y-axis
∴ Equation AB will be x=3
⇒x-3=0
And equation AB will be y=3
⇒y-3=0 (∵BC∥x-axis)
Chapter Test
1. Find the equation of a line whose inclination is 60° and y-intercept is – 4.
Solution:
We have given that: inclination = 60° and y-intercept (c) = -4
So, slope (m) = tan 60° = √3
Hence, the equation of the line is given by
y = mx + c
y = √3x – 4
2. Write down the gradient and the intercept on the y-axis of the line 3y + 2x = 12.
Solution:
We have given that:
Given line equation: 3y + 2x = 12
3y = -2x + 12
y = (-2/3) x + 12/3
y = (-2/3) x + 4
Hence, gradient = -2/3 and the intercept on the y-axis is 4.
3. If the equation of a line is y – √3x + 1, find its inclination.
Solution:
We have given that:
Given line equation: y – √3x + 1
y = √3x – 1
Here, slope = √3
⇒ tan θ = √3
θ = 60°
Hence, the inclination of the line is 60°.

