Refer to CBSE Class 9 Mathematics MCQs provided below available for download in Pdf. The MCQ Questions for Class 9 Mathematics with answers are aligned as per the latest syllabus and exam pattern suggested by CBSE, NCERT and KVS. Multiple Choice Questions for All Chapters are an important part of exams for Class 9 Mathematics and if practiced properly can help you to improve your understanding and get higher marks. Refer to more Chapter-wise MCQs for CBSE Class 9 Mathematics and also download more latest study material for all subjects
MCQ for Class 9 Mathematics All Chapters
Class 9 Mathematics students should refer to the following multiple-choice questions with answers for All Chapters in Class 9.
All Chapters MCQ Questions Class 9 Mathematics with Answers
Question. Certain number of persons comprising adults and children went to an exhibition. Entry ticket for the children is Rs 1.50 and Rs 4.50 for the adults. Total cost of the tickets come out to be Rs 600.
Which of the following pairs of numbers can be the number of adults and childre
(a) 90, 70
(b) 100, 60
(c) 110, 50
(d) 120, 40
Question. Mean of five observations is 7, on excluding two observations, the mean reduces to 6. On adding, the difference of the two excluded observations, the mean of the four observations becomes 25/4 .
What are the two excluded observations?
(a) 2, 9
(b) 6, 13
(c) 5, 12
(d) 8, 15
Question. Which of the following graph correctly represents the line 4x − 3y = 24? 
Question. The sum of squares of 100 observations was calculated as 7 961. Later, it was found that two values, 53 and 42, were wrongly read as 35 and 24, at the time of calculation. The corrected sum of squares is
(a) 10 730
(b) 10 733
(c) 11 730
(d) 11 733
Question. If a cone and a cylinder of same radii have the same volume, then what is the ratio of the heights of the cone and the cylinder?
(a) 1:1
(b) 1:2
(c) 2:1
(d) 3:1
Question. The given figure shows a circle with centre O. 
What is the measure of ∠OCA?
(a) 10°
(b) 15°
(c) 20°
(d) 25°
Question. A survey is conducted to know the number of mobile phones used in each family of a certain locality of 1000 families. The given data shows the results of the survey. 
What is the probability that a randomly chosen family has 4 mobile phones?
(a) 1/2
(b) 1/4
(c) 3/20
(d) 7/700
Question. What is the length of the line segment joining the mid points of the diagonals of a trapezium that is parallel to each of the parallel sides having lengths 12 cm and 4 cm.
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 6 cm
Question. The given figure shows a triangle ABC in which medians AD, BE, and CF intersect at point G. 
If the area of ΔABC is 30 cm2, then what is the area of the shaded region?
(a) 7.5 cm2
(b) 10 cm2
(c) 12.5 cm2
(d) 15 cm2
Question. Which of the following graphs correctly represents the line 3x + 4y = 12? 
Question. The arithmetic mean of a series of 20 items was calculated as 20. While calculating it, an item 13 was measured as 30. The correct arithmetic mean is
(a) 20.25
(b) 20.15
(c) 19.25
(d) 19.15
Question. A hemispherical bowl of thickness 0.7 cm is made up of a metal such that the inner radius of the bowl is 2.1 cm. The cost of the metal used is Rs 1.5 per cm3.
What is the approximate cost of the metal used to make such a bowl?
(a) Rs 30
(b) Rs 35
(c) Rs 40
(d) Rs 45
Question. The given figure shows a circle with centre O. 
What is the measure of ∠BOC?
(a) 45°
(b) 55°
(c) 70°
(d) 80°
Question. A die is thrown 400 times and the outcome of each throw is noted down. The given table shows the frequencies of the outcomes.
What is the probability of getting the number 5 in the next throw?
(a) 0.315
(b) 0.21
(c) 0.115
(d) 0.06
Question. The given figure shows a quadrilateral ABCD in which the diagonals AC and BD intersect each other at O. AB = BC, ∠AD = 25° and Area (ΔAOB) = Area (ΔCOD). 
What is the measure of ∠ABC?
(a) 130°
(b) 140°
(c) 145°
(d) 155°
Question. If a variable takes discrete values like x + 4, 
median is
(a) x-5/2
(b) x-1/2
(c) x-1/4
(d) x-5/4
Question. If a cone of height 24 cm is surmounted on a cylinder of radius 7 cm and height 30 cm, then what is the ratio of the curved surface area of the cone to that of the cylinder?
(a) 5:12
(b) 5:21
(c) 12:13
(d) 25:26
Question. The mean income of a group of workers is x̅ and that of another group of workers is y̅ . If the number of workers in the second group is 10 times the number of workers in the first group, then the mean income of the combined group of workers is 
Question. A cone and a cylinder have the same base are(a) The height and radius of these two solids are the same. If a sphere has the same radius as that of the cone, then what is the ratio of the volumes of the cone, the sphere and the cylinder?
(a) 1: 4: 1
(b) 1: 2: 1
(c) 1: 4: 3
(d) 1: 2: 3
Question. The straight line 2x − 5y = 5 meets the negative y-axis at a point whose coordinates are
(a) (0, − 3)
(b) (1, − 2)
(c) (1, − 2)
(d) (0, − 1)
Question. The mean of a set of numbers is x̅ . If each number is divided by 3, then the new mean is
(a) x̅
(b) x̅ + 3
(c) 3x̅
(d) x̅/3
Question. The total surface areas of the two hemispheres are in the ratio 25: 16. If the sum of their radii is 9 cm, then what are the respective radii of the two hemispheres?
(a) 8 cm and 1 cm
(b) 7 cm and 2 cm
(c) 6 cm and 3 cm
(d) 5 cm and 4 cm
Question. The arithmetic mean of n numbers is x̅ . If the sum of the first (n − 1) numbers is k, then the nth number is
(a) x̅ - k
(b) nx̅ - k
(c) x̅ - nk
(d) nx̅ - nk
Question. If a cone and a cylinder have the same base area and the same volume, then what is the ratio of their respective heights?
(a) 1: 1
(b) 3: 1
(c) 4: 9
(d) 9: 1
Question. The mean weight of a group of 6 students and a teacher is 41 kg. If the teacher is excluded from the group, then the mean weight gets reduced by 2.5 kg.
What is the weight of the teacher?
(a) 42 kg
(b) 45 kg
(c) 56 kg
(d) 57 kg
Question. If the radius of a sphere is increased by 10%, then what is the percentage increase in the surface area of the sphere?
(a) 10%
(b) 21%
(c) 100%
(d) 121%
Question. The given figure shows a circle with centre O. 
What is the measure of ∠APD?
(a) 20°
(b) 25°
(c) 30°
(d) 35°
Question. The given figure shows a circle with centre O, where XY is the tangent to the circle at point A. AB is the angle bisector of ∠XAC
What is the measure of ∠CAY?
(a) 65°
(b) 50°
(c) 45°
(d) 30°
Question. The given figure shows a parallelogram ABCD in which X and Y are the mid-points of sides AB and AD respectively. 
If the area of ΔCXY = 24 cm2, then what is the area of parallelogram ABCD?
(a) 32 cm2
(b) 48 cm2
(c) 64 cm2
(d) 96 cm2
Question. In the given figure, XY is the tangent at point C of the semi-circle with centre O. 
What is the measure of ∠BCY?
(a) 20°
(b) 30°
(c) 40°
(d) 50°
Question. The given figure shows a quadrilateral ABCD. A line drawn from A parallel to BD intersects CD produced at Q. BP is a line parallel to CQ such that QP ⊥ BP. 
If CQ = 22 cm and PQ = 5 cm, then what is the area of quadrilateral ABCD?
(a) 55 cm2
(b) 65 cm2
(c) 165cm2
(d) 220 cm2
Question. The given figure shows a circle with centre O. 
What is the measure of ∠DAC?
(a) 25°
(b) 45°
(c) 65°
(d) 75°
Question. In the given figure, ABCD is a rhombus and PQCB is a rectangle. 
If AC = 12 cm and BD = 16 cm, then what is the measure of PB?
(a) 8 cm
(b) 9.6 cm
(c) 10 cm
(d) 12.8 cm
Question. Ashu hired a cab in the night to go to a party. The cab provider told him that he will charge Rs 1000 for the cab and an extra charge of Rs 100 will be applicable for each hour after 12:00 a.m.
Ashu used the cab for x hours more after 12:00 a.m. If y is the total amount paid by Ashu, then which equation represents the given situation?
(a) y + 100x = 1000
(b) y + 1000 = 100x
(c) y = 1000 + 100x
(d) y + 100x + 1000 = 0
Question. What is the measure of ∠ABC in the given figure?
(a) 21°
(b) 31°
(c) 41.5°
(d) 48.5°
Question. The given figure shows a parallelogram PQRS in which A and B are any two points in the interior region. AS and BP intersect eachother at C, while AR and QB intersect each other at D. 
If area (ASBR) = 35 cm2 and area (ACBD) = 20 cm2, then what is the area of the shaded portion?
(a) 35 cm2
(b) 50 cm2
(c) 55 cm2
(d) 70 cm2
Question. What is the area of the region enclosed by the lines x = 0, y = 0 and x + y = 2?
(a) 3/2 square units
(b) 5/2 square units
(c) 2 square units
(d) 4 square units
Question. The ratio of radii of a cylinder and cone is 1: 3 and the ratio of their heights is 3: 4. What is the ratio of the volumes of the cylinder and the cone?
(a) 1: 4
(b) 3: 4
(c) 1: 9
(d) 4: 9
Question. What are the respective values of x and y in the given figure? 
(a) 40° and 45°
(b) 45° and 40°
(c) 135° and 165°
(d) 160° and 135°
Question. If (1, k) is a solution of the equation 2x + 5y = 12, then what is the value of k?
(a) −1
(b) -8/5
(c) 2
(d) 7/2
Question. What is the measure of ∠EFC in the given figure? 
(a) 59°
(b) 76°
(c) 104°
(d) 121°
Question. If the line ax + by + c = 0 is parallel to x-axis, then which of the following relations is correct?
(a) a = 0
(b) b = 0
(c) c = 0
(d) a = b
Question. A hemispherical tub is full of water. The water is to be emptied in cylindrical bottles. The radius of the cylindrical bottles is the same as that of the hemisphere. The height of the bottles is one-sixth of their radius.
How many cylindrical bottles can be filled from the water in the hemispherical tub?
(a) 2
(b) 4
(c) 6
(d) 8
Question. In the given figure, ΔABC is an isosceles triangle with AB = BC.
What are the respective measures of ∠EDC and ∠DEC?
(a) 64° and 18°
(b) 108° and 18°
(c) 116° and 64°
(d) 134° and 108°
Question. A metallic cylinder of radius 8 cm and height 20 cm is melted and recasted into 15 equal small spheres.
What is the diameter of each sphere?
(a) 2 cm
(b) 4 cm
(c) 8 cm
(d) 16 cm
Question. A circle with centre O is shown in the given figure. 
What is the measure of ∠BDC?
(a) 60°
(b) 80°
(c) 100°
(d) 120°
Question. The slant height and the curved surface area of a cone are 13 cm and 65π cm2 respectively. What is the volume of the cone?
(a) 49π cm3
(b) 95π cm3
(c) 100π cm3
(d) 169π cm3
Question. In the given figure, a circle with centre O is shown.
What is the measure of ∠BAC?
(a) 60°
(b) 80°
(c) 120°
(d) 160°
Question. The rule followed by the function table is 
(a) y = x − 1
(b) y = x − 2
(c) y = x − 3
(d) y = x − 4
Question. The mean weight of ten students is 35 kg. When two more students were included in the group, the mean increased by 1 kg.
If the weight of both the new students is the same, then what is the weight of each of the new students?
(a) 43 kg
(b) 41 kg
(c) 39 kg
(d) 37 kg
Question. In the given figure, XY = 6 cm and YZ = 8 cm. P and Q are the mid-points of XY and XZ respectively. 
What is the area of ΔXPQ?
(a) 6 cm2
(b) 8 cm2
(c) 12 cm2
(d) 14 cm2
Question. In parallelogram ABCD, AB = 20 cm and BC = 10 cm. P is the mid-point of side AB. A line through B parallel to PD meets CD at Q and AD produced at R. 
What is the measure of AR?
(a) 15 cm
(b) 17 cm
(c) 20 cm
(d) 30 cm
Question. The ages of Bob and his father are related by the expression y = 4x − 5 where x is Bob’s age and y is his father’s age.
Which of the following conclusions is true about the given expression?
(a) Bob’s father’s age is five less than four times Bob’s age
(b) Bob’s father’s age is four less than five times Bob’s age
(c) Bob’s father’s age is four times Bob’s age
(d) Bob’s father’s age as five times Bob’s age
Question. The mean of eight numbers is 21. If the mean of the first six numbers is 20 and the mean of the last six numbers is 21.5, then what is the mean of the middle four numbers?
(a) 18.5
(b) 19
(c) 20.25
(d) 23
Question. In the given figure, AB is the diameter of the circle with centre O and D is a point on the circle. C is a point on AD such that OC ⊥ AD. 
What is the perimeter of ΔABD if the perimeter of ΔAOC is 20 cm?
(a) 30 cm
(b) 40 cm
(c) 50 cm
(d) 60 cm
Question. What is the mean of the given frequency distribution? 
(a) 21.04
(b) 23.08
(c) 25.40
(d) 27.60
Question. In a class of 80 students, 25 students like to play hockey and 55 students like to play football. What is the probability that a randomly chosen student likes to play hockey?
(a) 11/16
(b) 5/8
(c) 3/8
(d) 5/16
Question. The given frequency distribution table shows the marks obtained by a group of students of a particular class. 
If the mean of the marks obtained by the students is 68.5, then what is the value of b?
(a) 7
(b) 6
(c) 4
(d) 3
Question. The given figure shows a circle with ∠XWY = 70° and ∠WZX = 30°. 
What is the measure of ∠WXY?
(a) 70°
(b) 80°
(c) 100°
(d) 110°
Question. The given figure represents a parallelogram PQRS in which PM and RN are perpendiculars drawn to the diagonal QS. 
If the area of the shaded region is 40 cm2, then what is the area of the parallelogram PQRS?
(a) 60 cm2
(b) 80 cm2
(c) 100 cm2
(d) 120 cm2
Question. Jack’s height is x inches and his brother’s height is y inches. Jack’s brother is one foot shorter than Jack.
Which of the following equations correctly represents the given situation?
(a) x = y + 1
(b) y = x + 1
(c) x = y + 12
(d) y = x + 12
Question. In the given figure, O is the centre of the circle. A, B and C are three points on the circle. 
If OC = 8.5 cm and AC = 8 cm, then what is the perimeter of ΔABC?
(a) 31.5 cm
(b) 38.5 cm
(c) 40 cm
(d) 47 cm
Question. The given figure shows a trapezium PQRS in which PQ||SR. A and B are the mid-points of diagonals QS and PR respectively. 
What is the length of AB?
(a) 5 cm
(b) 6 cm
(c) 7.5 cm
(d) 8.1 cm
Question. What is the value of (∠AOB − ∠ACB)? 
(a) 15°
(b) 20°
(c) 25°
(d) 30°
Question. If the mean of the given distribution is 4.7, then what is the value of m? 
(a) 5
(b) 6
(c) 11
(d) 14
Question. Two coins are simultaneously tossed 200 times and the following table is obtained. 
What is the probability of getting two tails.
(a) 0.13
(b) 0.26
(c) 0.39
(d) 0.52
Question. The mean of thirty numbers is 25. If 15 is subtracted from each of the first 12 numbers and 15 is added to each of the last 18 numbers, then what will be the mean of the new set of numbers?
(a) 32
(b) 31
(c) 28
(d) 23
Question. The mean weight of all girls of a class is 36 kg and that of the boys of the class is 42 kg. The mean weight of all the students of the class is 40 kg.
What is the ratio of the number of girls and boys in the class?
(a) 1:2
(b) 1:4
(c) 2:3
(d) 3:4
Question. What is the mean of the first five multiples of both the numbers 10 and 3?
(a) 90
(b) 95
(c) 105
(d) 120
Question. A die is thrown 3000 times and its outcome is noted each time. The given table lists the number of times each number appeared on the die. 
If the same coin is tossed again, then what is the probability of getting an even number on the die?
(a) 121/300
(b) 137/300
(c) 163/300
(d) 173/300
Question. The mean of the numbers 21, 30, 16, x, and 9 is 18. The median of the numbers 23, 30, 31, 3x, 3x + y, 60, 67, and 69 is 47.5.
What is the value of y?
(a) 11
(b) 14
(c) 33
(d) 42
Question: If (2,-3) is solution of eqn 3x-ky=2 then the value of K is
a) -2
b) -2/3
c) -4
d) -4/3
Answer: -4/3
Question: If the slant height of a cone is 10 cm and its radius is 6cm, then height of cone is
a) 9cm
b) 13cm
c) 16cm
d) 8cm
Answer: 8cm
Question: If the lateral surface area of cube is 1600cm2 then its edge is
a) 15cm
b) 18cm
c) 25cm
d) 20cm
Answer: 20cm
Question: Which one is solution of eqn x-3y=2
a) (4,1)
b) (6,2)
c) (5,1)
d) (0,2)
Answer: (5,1)
Question: A die is thrown once. The probability of getting an even no. is
a) 1/2
b) 1/3
c) 1/5
d) 2
Answer: 1/2
Question: Class mark of class interval 90-110 is
a) 90
b) 110
c) 100
d) None
Answer: 100
Question: Three angle of a quadrilateral is 60°, 110° and 86°. The fourth angle of quadrilateral is
a) 104°
b) 124°
c) 94°
d) 84°
Answer: 104°
Question: The value of x in the given figure is
a) 22°
b) 33°
c) 44°
d) 68°
Answer: 22°
Question: Which was the Tabled city of gold?
a) Peru
b) Mexico
c) El Doeodo
d) Spain
Answer: El Doeodo
Question: Which of the following is an irrational number?
a) 3.14
b) 3.141
c) 3.1411
d) 3.141141114
Answer: 3.141141114
Question: The zeros of the polynomial p(x)=x2+x-6 are
a) 2,3
b) -2, 3
c) 2,-3
d) -2, -3
Answer: 2,-3
Question: The value of k, for which the polynomial x3-3x2+3x+k has 3 as its zero, is
a) -3
b) 9
c) -9
d) 12
Answer: -9
Question: When (x31+31) is divided by (x+1) the remainder is
a) 0
b) 1
c) 30
d) 31
Answer: 30
Question: In the given figure, AOB is a straight line. If
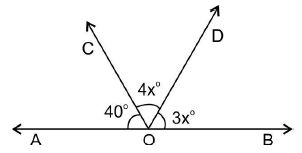
a) 80°
b) 100°
c) 120°
d) 140°
Answer: 80°
Question: In the figure ABC is an equilateral triangle and BDC is an isosceles right triangle, right angled at D,
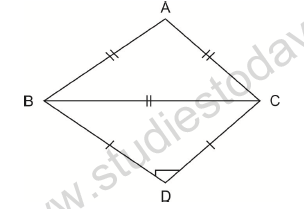
a) 45°
b) 60°
c) 105°
d) 120°
Answer: 105°
Question: In a
a) 60cm2
b) 30cm2
c) 15√3cm2
d) 45cm2
Answer: 30cm2
Question: The perimeter of an equilateral triangle is 60m. The area is
a) 100√3 m2
b) 10√3 m2
c) 15√4 m2
d) 20√3 m2
Answer: 100√3 m2
a) 80°
b) 100°
c) 120°
d) 140°
Answer: 80°
Question: In the figure ABC is an equilateral triangle and BDC is an isosceles right triangle, right angled at D,
a) 45°
b) 60°
c) 105°
d) 120°
Answer: 105°
Question: In a
a) 60cm2
b) 30cm2
c) 15√3cm2
d) 45cm2
Answer: 30cm2
Question: The perimeter of an equilateral triangle is 60m. The area is
a) 100√3 m2
b) 10√3 m2
c) 15√4 m2
d) 20√3 m2
Answer: 100√3 m2
a) 45°
b) 60°
c) 105°
d) 120°
Answer: 105°
Question: In a
a) 60cm2
b) 30cm2
c) 15√3cm2
d) 45cm2
Answer: 30cm2
Question: The perimeter of an equilateral triangle is 60m. The area is
a) 100√3 m2
b) 10√3 m2
c) 15√4 m2
d) 20√3 m2
Answer: 100√3 m2
Question: The number of planks of dimensions (4 m × 50 cm × 20 cm) that can be stored in a pit which is 16 m long, 12m wide and 4 m deep is
a) 1900
b) 1920
c) 1800
d) 1840
Answer: 1920
Question: In a cylinder, radius is doubled and height is halved, curved surface area will be
a) halved
b) doubled
c) same
d) four times
Answer: doubled
Question: The marks obtained by 17 students in a mathematics test (out of 100) are given below : 91, 82, 100, 100, 96, 65, 82, 76, 79, 90, 46, 64, 72, 68, 66, 48, 49. The range of the data is :
a) 46
b) 54
c) 90
d) 100
Answer: 54
Question: The equation 2x + 5y = 7 has a unique solution, if x, y are :
a) Natural numbers
b) Positive real numbers
c) Real numbers
d) Rational numbers
Answer: Natural numbers
Question: AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is :
a) 17 cm
b) 15 cm
c) 4 cm
d) 8 cm
Answer: 15 cm
Question: In Δ ABC, BC = AB and ∠B = 80°. Then ∠A is equal to
a) 80°
b) 40°
c) 50°
d) 100°
Answer: 50°
Question: Abscissa of all the points on the x-axis is
a) 0
b) 1
c) 2
d) any number
Answer: any number
Question: Two coins are tossed 1000 times and the outcomes are recorded as below :
a) 1/5
b) 1/4
c) 4/5
d) 3/4
Answer: 3/4
Question: Point (– 10, 0) lies
a) on the negative direction of the x-axis
b) on the negative direction of the y-axis
c) in the third quadrant
d) in the fourth quadrant
Answer: on the negative direction of the x-axis
Question: In Δ ABC, AB = AC and ∠B = 50°. Then ∠C is equal to
a) 40°
b) 50°
c) 80°
d) 130°
Answer: 50°
Question: ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to:
a) 80°
b) 50°
c) 40°
d) 30°
Answer: 40°
Question: The linear equation 2x – 5y = 7 has
a) A unique solution
b) Two solutions
c) Infinitely many solutions
d) No solution
Answer: Infinitely many solutions
Question: The class-mark of the class 130-150 is :
a) 130
b) 135
c) 140
d) 145
Answer: 140
Question: The radii of two cylinders are in the ratio of 2:3 and their heights are in the ratio of 5:3. The ratio of their volumes is:
a) 10 : 17
b) 20 : 27
c) 17 : 27
d) 20 : 37
Answer: 20 : 27
Question: Two coins are tossed 1000 times and the outcomes are recorded as below :
a) 1/5
b) 1/4
c) 4/5
d) 3/4
Answer: 3/4
Question: In a cylinder, radius is doubled and height is halved, curved surface area will be
a) halved
b) doubled
c) same
d) four times
Answer: doubled
Question: Signs of the abscissa and ordinate of a point in the second quadrant are respectively
a) +,+
b) -,-
c) -,+
d) +,-
Answer: -,+
Question: Which of the following is not a criterion for congruence of triangles?
a) SAS
b) ASA
c) SSA
d) SSS
Answer: SSA
Question: If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is :
a) 6
b) 8
c) 10
d) 12
Answer: 10
Question: Any point on the y-axis is of the form
a) (x, 0)
b) (x, y)
c) (0, y)
d) ( y, y)
Answer: (0, y)
Question: The range of the data : 25, 18, 20, 22, 16, 6, 17, 15, 12, 30, 32, 10, 19, 8, 11, 20 is
a) 10
b) 15
c) 18
d) 26
Answer: 26
Question: The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratios of the surface areas of the balloon in the two cases is
a) 1 : 4
b) 1 : 3
c) 2 : 3
d) 2 : 1
Answer: 1 : 4
Question: In a survey of 364 children aged 19-36 months, it was found that 91 liked to eat potato chips. If a child is selected at random, the probability that he/she does not like to eat potato chips is :
a) 0.25
b) 0.50
c) 0.75
d) 0.80
Answer: 0.75
Question: The length of the longest pole that can be put in a room of dimensions (10 m × 10 m × 5m) is
a) 15 m
b) 16 m
c) 10 m
d) 12 m
Answer: 15 m
Question: Point (0, –7) lies
a) on the x –axis
b) in the second quadrant
c) on the y-axis
d) in the fourth quadrant
Answer: on the y-axis
Question: If AB = QR, BC = PR and CA = PQ, then
a) Δ ABC ≅ Δ PQR
b) Δ CBA ≅ Δ PRQ
c) Δ BAC ≅ Δ RPQ
d) Δ PQR ≅ Δ BCA
Answer: Δ CBA ≅ Δ PRQ
More Questions.........................
Question: AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is:
a) 17 cm
b) 15 cm
c) 4 cm
d) 8 cm
Answer: 8 cm
Question: A linear equation in two variables is of the form ax + by + c = 0, where
a) a ≠ 0, b ≠ 0
b) a = 0, b ≠ 0
c) a ≠ 0, b = 0
d) a = 0, c = 0
Answer: a = 0, b ≠ 0
Question: The class mark of the class 90-120 is :
a) 90
b) 105
c) 115
d) 120
Answer: 105
Question: The number of planks of dimensions (4 m × 50 cm × 20 cm) that can be stored in a pit which is 16 m long, 12m wide and 4 m deep is
a) 1900
b) 1920
c) 1800
d) 1840
Answer: 1920
Question: In a medical examination of students of a class, the following blood groups are recorded:
a) 1/4
b) 13/40
c) 3/10
d) 1/8
Answer: 3/10
Question: The lateral surface area of a cube is 256 m2. The volume of the cube is
a) 512 m3
b) 64 m3
c) 216 m3
d) 256 m3
Answer: 512 m3
Question: 9sec2 A – 9 tan2A is :
a) 1
b) 9
c) 8
d) 0
Answer: 9
Question: Point (–3, 5) lies in the
a) first quadrant
b) second quadrant
c) third quadrant
d) fourth quadrant
Answer: second quadrant
Question: If Δ ABC ≅ Δ PQR and Δ ABC is not congruent to Δ RPQ, then which of the following is not true:
a) BC = PQ
b) AC = PR
c) QR = BC
d) AB = PQ
Answer: BC = PQ
Question: ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to:
a) 80º
b) 50º
c) 40º
d) 30º
Answer: 40º
Question: The linear equation 3x – y = x – 1 has :
a) A unique solution
b) Two solutions
c) Infinitely many solutions
d) No solution
Answer: Infinitely many solutions
Question: The width of each of five continuous classes in a frequency distribution is 5 and the lower class-limit of the lowest class is 10. The upper class-limit of the highest class is:
a) 15
b) 25
c) 35
d) 40
Answer: 35
Question: In a cylinder, if radius is halved and height is doubled, the volume will be
a) Same
b) doubled
c) halved
d) four times
Answer: doubled
Question: In a sample study of 642 people, it was found that 514 people have a high school certificate. If a person is selected at random, the probability that the person has a high school certificate is :
a) 0.5
b) 0.6
c) 0.7
d) 0.8
Answer: 0.8
Question: The total surface area of a cube is 96 cm2. The volume of the cube is:
a) 8 cm3
b) 512 cm3
c) 64 cm3
d) 27 cm3
Answer: 64 cm3
Question: Point (–3, 5) lies in the
a) first quadrant
b) second quadrant
c) third quadrant
d) fourth quadrant
Answer: second quadrant
Question: If Δ ABC ≅ Δ PQR and Δ ABC is not congruent to Δ RPQ, then which of the following is not true:
a) BC = PQ
b) AC = PR
c) QR = BC
d) AB = PQ
Answer: BC = PQ
Question: ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to:
a) 80º
b) 50º
c) 40º
d) 30º
Answer: 40º
Question: The linear equation 3x – y = x – 1 has :
a) A unique solution
b) Two solutions
c) Infinitely many solutions
d) No solution
Answer: Infinitely many solutions
Question: The width of each of five continuous classes in a frequency distribution is 5 and the lower class-limit of the lowest class is 10. The upper class-limit of the highest class is:
a) 15
b) 25
c) 35
d) 40
Answer: 35
Question: The total surface area of a cube is 96 cm2. The volume of the cube is:
a) 8 cm3
b) 512 cm3
c) 64 cm3
d) 27 cm3
Answer: 64 cm3
Question: In a sample study of 642 people, it was found that 514 people have a high school certificate. If a person is selected at random, the probability that the person has a high school certificate is :
a) 0.5
b) 0.6
c) 0.7
d) 0.8
Answer: 0.8
Question: In a cylinder, if radius is halved and height is doubled, the volume will be
a) Same
b) doubled
c) halved
d) four times
Answer: doubled
Question: The width of each of five continuous classes in a frequency distribution is 5 and the lower class-limit of the lowest class is 10. The upper class-limit of the highest class is:
a) 15
b) 25
c) 35
d) 40
Answer: 35
Question: Which of the following cannot be empirical probability of an event?
a) 4/5
b) 1
c) 0
d) 5/4
Answer: 5/4
Question: If the volume of a sphere is numerically equal to its surface area, then radius of the sphere is
a) 1 unit
b) 3 units
c) 2 units
d) 6 units
Answer: 3 units
Question: In a frequency distribution, the mid-value of a class is 20 and the width of the class is 8. then the lower limit of the class is
a) 12
b) 24
c) 28
d) 16
Answer: 16
Question: Equation of x-axis is
a) x = 0
b) x = y
c) y = 0
d) x + y = 0
Answer: y = 0
Question: The median of a triangle divides it into two
a) triangles of equal area
b) equilateral triangles
c) right triangles
d) isosceles triangles
Answer: triangles of equal area
Question: Sum of exterior angles of a triangle is :
a) 270°
b) 306°
c) 630°
d) 360°
Answer: 360°
Question: Which one is correct order of Cartesian plane for the points (4, –4), (–3, 2), (–5, – 7) and (6, 3)?
a) I, II, III, IV
b) IV, II, III, I
c) III, II, I, IV
d) II, III, IV, I
Answer: IV, II, III, I
Question: What is the remainder when polynomial x3 – ax2 + 6x – a is divided by (x – a)?
a) a
b) 3a
c) a/5
d) 5a
Answer: 5a
Question: What are the zeroes of the polynomial x2 – 16?
a) (4, –4)
b) (–4, –4)
c) (4, 4)
d) None of these
Answer: (4, –4)
Question: A bag contains 7 red balls, 6 green balls, 4 black balls. A ball is drawn randomly from this bag. What is the probability of the drawn ball is to be white ball?
a) 7/17
b) 6/17
c) 4/17
d) 0
Answer: 0
Question: Find the area of equilateral triangle of side 4 cm.
a) 4√3 cm
b) 4√3 cm
c) 3√4 cm
d) 6cm
Answer: 4√3 cm
Question: [(64)1/2 x (1/27)1/3]2
a) 2
b) 9
c) 9/2
d) 2/9
Answer: 2/9
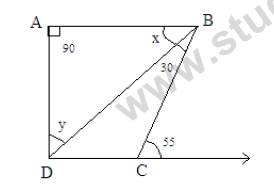
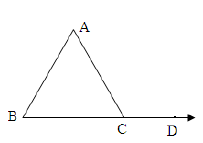
Question: In the given figure if
a) 54°
b) 126°
c) 136°
d) 108°
Answer: 126°
Question: If DC AA || AB, the values of ‘x’ and ‘y’ are :
a) (45°, 25°)
b) (25°, 65°)
c) (30°, 45°)
d) (45°, 30°)
Answer: (25°, 65°)
Question: In the given figure if
a) 54°
b) 126°
c) 136°
d) 108°
Answer: 126°
Question: In circle (O, r) AB is the chord and o, find
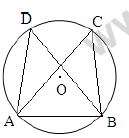
a) 67°
b) 78°
c) 87°
d) 76°
Answer: 76°
a) 54°
b) 126°
c) 136°
d) 108°
Answer: 126°
Question: If DC AA || AB, the values of ‘x’ and ‘y’ are :
a) (45°, 25°)
b) (25°, 65°)
c) (30°, 45°)
d) (45°, 30°)
Answer: (25°, 65°)
Question: In the given figure if
a) 54°
b) 126°
c) 136°
d) 108°
Answer: 126°
Question: In circle (O, r) AB is the chord and o, find
a) 67°
b) 78°
c) 87°
d) 76°
Answer: 76°
a) 54°
b) 126°
c) 136°
d) 108°
Answer: 126°
Question: In circle (O, r) AB is the chord and o, find
a) 67°
b) 78°
c) 87°
d) 76°
Answer: 76°
a) 67°
b) 78°
c) 87°
d) 76°
Answer: 76°
| CBSE Class 9 Maths Number Systems MCQs |
| CBSE Class 9 Maths Polynomials MCQs |
| CBSE Class 9 Maths Coordinate Geometry MCQs |
| CBSE Class 9 Maths Linear Equations in Two Variables MCQs |
| CBSE Class 9 Maths Introduction to Euclids Geometry MCQs |
| CBSE Class 9 Maths Lines and Angles MCQs |
| CBSE Class 9 Maths Triangles MCQs |
| CBSE Class 9 Maths Quadrilaterals MCQs |
| CBSE Class 9 Maths Areas of Parallelogram and Triangle MCQs |
| CBSE Class 9 Maths Circles MCQs |
| CBSE Class 9 Maths Constructions MCQs |
| CBSE Class 9 Maths Herons Formula MCQs |
| CBSE Class 9 Maths Surface Areas and Volumes MCQs |
| CBSE Class 9 Maths Statistics MCQs |
| CBSE Class 9 Maths Probability MCQs |
| CBSE Class 9 Mathematics MCQs |
| CBSE Class 9 Quantitative Reasoning MCQs |
MCQs for Mathematics CBSE Class 9 All Chapters
Expert teachers of studiestoday have referred to NCERT book for Class 9 Mathematics to develop the Mathematics Class 9 MCQs. If you download MCQs with answers for the above chapter daily, you will get higher and better marks in Class 9 test and exams in the current year as you will be able to have stronger understanding of all concepts. Daily Multiple Choice Questions practice of Mathematics and its study material will help students to have stronger understanding of all concepts and also make them expert on all critical topics. After solving the questions given in the MCQs which have been developed as per latest course books also refer to the NCERT solutions for Class 9 Mathematics designed by our teachers
All Chapters MCQs Mathematics CBSE Class 9
All MCQs given above for Class 9 Mathematics have been made as per the latest syllabus and books issued for the current academic year. The students of Class 9 can refer to the answers which have been also provided by our teachers for all MCQs of Mathematics so that you are able to solve the questions and then compare your answers with the solutions provided by us. We have also provided lot of MCQ questions for Class 9 Mathematics so that you can solve questions relating to all topics given in each chapter. All study material for Class 9 Mathematics students have been given on studiestoday.
All Chapters CBSE Class 9 MCQs Mathematics
Regular MCQs practice helps to gain more practice in solving questions to obtain a more comprehensive understanding of All Chapters concepts. MCQs play an important role in developing understanding of All Chapters in CBSE Class 9. Students can download and save or print all the MCQs, printable assignments, practice sheets of the above chapter in Class 9 Mathematics in Pdf format from studiestoday. You can print or read them online on your computer or mobile or any other device. After solving these you should also refer to Class 9 Mathematics MCQ Test for the same chapter
CBSE MCQs Mathematics Class 9 All Chapters
CBSE Class 9 Mathematics best textbooks have been used for writing the problems given in the above MCQs. If you have tests coming up then you should revise all concepts relating to All Chapters and then take out print of the above MCQs and attempt all problems. We have also provided a lot of other MCQs for Class 9 Mathematics which you can use to further make yourself better in Mathematics
You can download the CBSE MCQs for Class 9 Mathematics All Chapters for latest session from StudiesToday.com
Yes, you can click on the links above and download topic wise MCQs Questions PDFs for All Chapters Class 9 for Mathematics
Yes, the MCQs issued by CBSE for Class 9 Mathematics All Chapters have been made available here for latest academic session
You can easily access the links above and download the All Chapters Class 9 MCQs Mathematics for each topic
There is no charge for the MCQs and their answers for Class 9 CBSE Mathematics All Chapters you can download everything free
Regular revision of MCQs given on studiestoday for Class 9 subject Mathematics All Chapters can help you to score better marks in exams
Multiple Choice Questions (MCQs) for All Chapters Class 9 Mathematics are objective-based questions which provide multiple answer options, and students are required to choose the correct answer from the given choices.
Learning All Chapters based MCQs will help students improve their overall understanding of important concepts and topics and help to score well in Class 9 Mathematics exams.
You can practice All Chapters for CBSE Class 9 through worksheets, textbooks and online quizzes provided by studiestoday.com.
You can find CBSE Class 9 Mathematics All Chapters MCQs on educational websites like studiestoday.com, online tutoring platforms, and in sample question papers provided on this website.
To prepare for All Chapters MCQs, refer to the concepts links provided by our teachers and download sample papers for free.
Yes, there are many online resources that we have provided on studiestoday.com available such as practice worksheets, question papers, and online tests for learning MCQs for Class 9 Mathematics All Chapters
Yes, you can find printable All Chapters worksheets for CBSE Class 9 Mathematics on studiestoday.com.
We have provided full database of free multiple choice questions with answers on studiestoday.com for CBSE Class 9 Mathematics All Chapters