CBSE Class 10 Maths HOTs Trigonometry

CASE STUDY 

Mohan, a class X student is a big foodie. Once his mother has made a sandwich for him. A thought has come into his mind by seeing a piece of sandwich. He thought if he increases the base length and height, he can eat a bigger piece of sandwich.
Answer the following questions accordingly:

Question. If the length of the base is 12 cm and the height is 5 cm then the length of the hypotenuse of that sandwich is:
(a) 17 cm
(b) 7 cm
(c) 169 cm
(d) 13
Answer : D

Question. 2.What will be the value of cosine of the angle between hypotenuse and the height of sandwich?
(a) (5/13)cm
(b) (12/13)cm
(c) (13/5)cm
(d) (13/12)cm
Answer : A

Question. If he increases the base length to 15 cm and the hypotenuse to 17 cm, then the height of the sandwich is :
(a) 7 cm
(b) 8 cm
(c) 32 cm
(d) none of these
Answer : B

Question. If the value of tan θ is √3, then sin- equals to:
(a) 1/√2
(b) √3/2
(c) 1/2
(d) 1
Answer : B

Question. The value of tan 45° + cot 45°
(a) 1
(b) 2
(c) 3
(d) 4
Answer : B

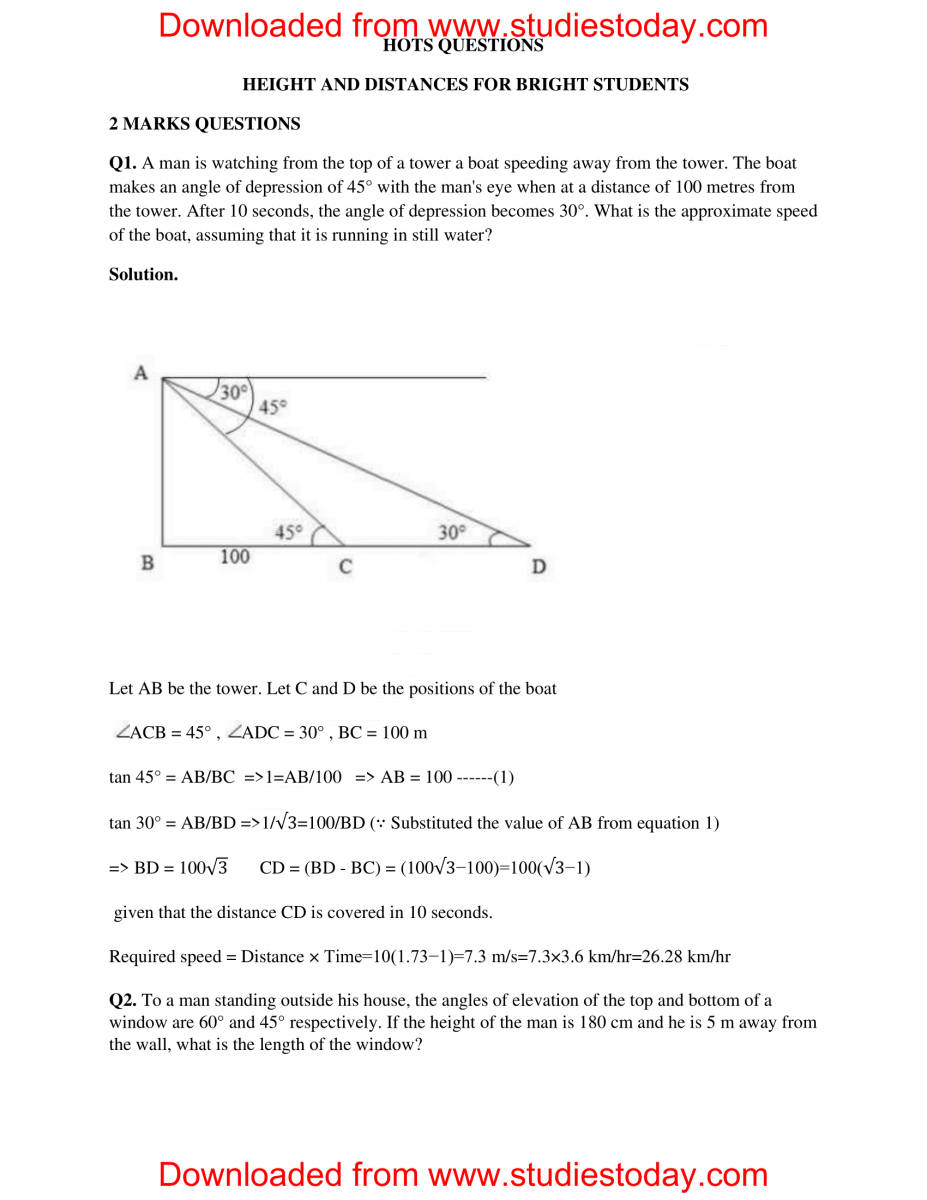
Three friends Ashwin, Bhagath & Amal are playing hide and seek in a park. Ashwin, Bhagath hide in the shrubs and Amal have to find both of them. If the positions of three friends are at A, B and C respectively as shown in the figure and forms a right-angled triangle, such that AB =9 m, BC= 3√3 m and ∠𝐵 =90°.Now answer the following questions

On the basis of above answer the following questions

Question. The measure of ∠ 𝐴 is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer : A

Question. The measure of ∠𝐶 is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer : C

Question. The length of AC is
(a) 8√2
(b) 6√3
(c) 4√2
(d) 2√3
Answer : B

Question. cos2𝐴=
(a) 0
(b) 1/2
(c) 1/√2
(d) √3/2
Answer : B

Question. sin(𝐶/2) =
(a) 0
(b) 1/2
(c) 1/√2
(d) √3/2
Answer : B

Please refer to link below to download pdf file of CBSE Class 10 Trigonometry HOTs.

ADDITIONAL QUESTION

Please refer to link below for CBSE Class 10 Mathematics HOTs Trigonometry Set A.

Please refer to link below to download pdf file of CBSE Class 10 Mathematics HOTs Trigonometry

 

Q2 From the figure find the value of sin x and cos y.

 

Q3 If 5 tan θ – 4 = θ, then find the value of 5 sin θ – 4 cos θ/5 sin θ + 4 cos θ 

 

Q4 In ∆ ABC,  ∠c = 90°, tan A =   1/√3 and tan B = √3. Prove that sinA .cosB + cos A .sin B =1. 

 

Q5. If  ∠XAC = 45°, find the value of x and y in the figure

 

Q. 16 If tan (3x –15⁰ ) =1, than write the value of 'x'.

 

Q. 17 In ΔABC, write tan A+ B/2  in terms of angle 'C'.

 

Q. 18 If θ = 30⁰ , then write the value of 1 – tan² 2θ .

 

Q. 19 If tanθ + cotθ = 3 , then what is the value of tan²θ + cot²θ ?

 

Q 20 Write the value of cot (35⁰ +θ ) – tan (55⁰ –θ )

 

2 marks questions (Question 36 to 40 under HOTS)

 

Q. 21 If sin 2θ = cos (θ – 36)⁰ , 2θ and (θ – 36⁰ ) are acute angles. Find the value of 'θ ' .

 

Q. 22 If tan (32⁰ +θ ) = cotθ , θ and (32⁰ +θ ) are acute angles, find the value of 'θ '.

 

Q. 23 If sin ( A+ B) =1 and ( ) cos (A – B) √3 /2  = , 0⁰ ≤ ( A+ B) ≤ 90⁰ , A > B, then find the values of A and B.

 

Q. 24 If θ = 30⁰ , then find the value of 1 - Tan²θ / 1 + Tan²θ

 

Q. 25 If tanθ = √2 –1, then find the value of  2 tanθ/1 + tan²θ

 

Q. 26 If θ = 30⁰ , then verify : cos3θ = 4cos³θ – cosθ .

 

Q. 27 Simplify : tan² 60⁰ + 4cos2 45⁰ + 3sec2 30⁰ + 5cos2 90⁰

 

6 marks questions (Question no. 76 to 80 under HOTS)

Q. 61 From a point on the ground the angles of elevation of the bottom and the top of a water tank kept at the top of 30 m high building are 45⁰ and 60⁰ respectively. Find the height of the water tank.

Q. 62 A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 60⁰ with the ground. The distance from the foot of the tree to the point where the top touches the ground is 2m. Find total height of the tree.

Q. 63 The shadow of a tower standing on a level ground is found to be 60m shorter when the sun's altitude is 60⁰ than when it is 30⁰ , find the height of the tower.

Q. 64 The angles of elevation of the top of a pole, from two points A and B at distances of 'a' and 'b' respectively from the base and in the same straight line with it, are complementary. Prove that the height of the pole is √ab .

Q. 65 The angles of elevation of a cloud from a point 30m above a lake is 30⁰ and the angle of depression of its reflection in the lake is 60⁰ . Find the height of the cloud above th lake.

Q. 66 The angles of elevation of a bird from a point on the ground is 60⁰ , after 50 seconds flight, the elevation changes to 30⁰ . If the bird is flying at the height of 500 √3m . Find the speed of the bird.

Q. 67 If the angle of elevation of a bird from a point metres above a Jake is α and the angle of depression of its reflection in the lake is β . Prove that the distance of the bird from the point of observation is 2a sec α /tanβ – tan α .

Q. 68 The angle of elevation of the top of a 12m tall building from a point A on the ground is 30⁰ .A flag is hoisted at the top of the building and the angle of elevation of the flag staff from A is 45⁰ . Find the length of flag staff and the distance of the building from A.

 

Q. 69 The angles of depression of the top and bottom of a 10m tall building from the top of a tower are 30⁰  and 45⁰  respectively. Find the height of opposite house.

 

Q. 70 From a window (60m high above the ground) of a house in a street, the angles of elevation and depression of the top and the foot of an other house opposite side of street are 60⁰  and 45⁰  respectively. Find the height of the opposite house.

 

Q. 71 A man on the deck of a ship, 18 m above water level, observes that the angle of elevation and depression respectively of the top and bottom of a cliff are 60⁰  and 30⁰  . Find the distance of the cliff from the ship and height of the cliff.

 

Q. 72 A flight pole 4m high is fixed on the top of a tower. The angle of elevation of the top of the pole observed from a point 'A' on the ground is 60⁰  and the angle of depression of the point 'A' from the top of the tower is 45⁰  . Find the height of the tower.

 

Q. 73 A man, on a cliff, observes a boat at an angle of depression of 30⁰  which is approaching the shore to the point 'A' on the immediately beneath the observer with a uniform speed, 12 minutes later, the angle of depression of the boat is found to be 60⁰  . Find the time taken by the boat to reach the shore.

 

Q. 74 A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank, is 60⁰  , when he retires 30 metres from the bank, he finds the angle to be 30⁰  . Find the breadth of the river and height of the tree.

 

Q. 75 An aeroplane at an altitude of 100m observes the angles of depression of opposite points on the two banks of a river to be 30⁰ and 45⁰  . Find the width of the river.

 

Q. 76 A round balloon of radius 'r' subtends an angle Q at the eye of the observer while the angle of elevation of its centre is α . Prove that the height of the centre of the balloon is rsin αcosec θ/2

 

Q. 77 A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance m, so that it slides a distance n down the wall making an angle β with horizontal, show that :- m/n = cosβ - cosα / sinα - sinβ.

 

Q. 78 From an aeroplane vertically above a straight horizontal plane, the angle of depression of two consecutive kilometer stones on the opposite sides of the aeroplane are found to be θ and φ . Show that the height of the aeroplane is

tanθ .tanφ / tanθ + tanφ

 

Q. 79 At the foot of the mountain the elevation of its summit is 45⁰ . After ascending 1000 metres towards the mountain at an inclination of 30⁰ , the elevation is 60⁰ . Calculate the height of the mountain.

 

Q. 80 At a point P on level grounds, the angle of elevation of a vertical tower is found to be such that its tangent is 3/4 . On walking 192 metres away from P the tangent of the angle is 5/1 2 .Find the height of the tower.