Refer to BITSAT Mathematics Conic Sections MCQs provided below. BITSAT Full Syllabus Mathematics MCQs with answers available in Pdf for free download. The MCQ Questions for Full Syllabus Mathematics with answers have been prepared as per the latest syllabus, BITSAT books and examination pattern suggested in Full Syllabus by BITSAT, NCERT and KVS. Multiple Choice Questions for Conic Sections are an important part of exams for Full Syllabus Mathematics and if practiced properly can help you to get higher marks. Refer to more Chapter-wise MCQs for BITSAT Full Syllabus Mathematics and also download more latest study material for all subjects
MCQ for Full Syllabus Mathematics Conic Sections
Full Syllabus Mathematics students should refer to the following multiple-choice questions with answers for Conic Sections in Full Syllabus. These MCQ questions with answers for Full Syllabus Mathematics will come in exams and help you to score good marks
Conic Sections MCQ Questions Full Syllabus Mathematics with Answers
Question: Find the equation of the hyperbola whose directrix is 2x + y = 1, focus (1, 2) and eccentricity √3
- a) 7x2 – 2y2 + 12xy – 2x – 14 – 22 = 0
- b) 7x2 + 2y2 – 12xy – 2x + 14 – 22 = 0
- c) 7x2 + 2y2 + 12xy – 2x – 14 – 22 = 0
- d) 7x2 – 2y2 + 12xy – 2x + 14 – 22 = 0
Answer: 7x2 – 2y2 + 12xy – 2x + 14 – 22 = 0
Question: Find the parametric coordinates of any point of the circle x2 + y2 + 2x – 3y – 4 = 0
- a)
- b)
- c)
- d)
Answer:
Question: If the tangent at the point P(x1, y1) to the parabola y2 = 4ax meets the parabola y2 = 4a(x + b) at Q and R, then the mid-point of QR is
- a) (x1 + b, y1 + b)
- b) (x1 – b, y1 – b)
- c) (x1, y1)
- d) (x1 + b, y1)
Answer: (x1, y1)
Question: If the line 3x + ay – 20 = 0 cuts the circle x2 + y2 = 25 at real distinct or coincident points, then a belongs to the interval
- a) [- √7, √7]
- b) (- √7, 1/7)
- c)
- d) None of these
Answer:
Question: The total number of common tangents to the two circles x2 + y2 – 2x – 6y + 9 = 0 and x2 + y2 + 6x – 2y + 1 = 0, is -
- a) 1
- b) 2
- c) 3
- d) 4
Answer: 4
Question: The equation of the tangent to the elipse x2 + 4y2 = 25 at the point whose ordinate is 2 is
- a) x + 2y = 5 or 2x - y = 5
- b) 3x +8y = 25 or 8y -3x = 25
- c) 3x + 2y =15 or 3y - 2x =15
- d) None of these
Answer: 3x +8y = 25 or 8y -3x = 25
Question: An equilateral triangle is inscribed in the circle x2 + y2 = a2 with one of the vertices at (a, 0). What is the equation of the side opposite to this vertex ?
- a) 2x – a = 0
- b) x + a = 0
- c) 2x + a = 0
- d) 3x – 2a = 0
Answer: 2x + a = 0
Question: The equation of one of the common tangents to the parabola y2 = 8x and x2 + y2 -12x + 4 = 0 is
- a) y = –x + 2
- b) y = x – 2
- c) y = x + 2
- d) None of these
Answer: y = x + 2
Question: The line joining (5, 0) to ( (10cos θ, 10sin θ) is divided internally in the ratio 2 : 3 at P. If θ varies, then the locus of P is
- a) A pair of straight
- b) A circle lines
- c) A straight line
- d) None of these
Answer: A circle lines
Question: The number of integral values of λ for which x2 + y2 + λx + (1- λ)y + 5 = 0 is the equation of a circle whose radius cannot exceed 5, is
- a) 14
- b) 18
- c) 16
- d) None of these
Answer: 16
Question: An ellipse has OB as semi minor axis, F and F ' its focii and the angle FBF ' is a right angle. Then the eccentricity of the ellipse is
- a)
- b)
- c)
- d)
Answer:
Question: If the line 2x – 3y = k touches the parabola y2 = 6x, then find the value of k
- a) –15/4
- b) –27/4
- c) –1/4
- d) –3/4
Answer: –27/4
Question: S and T are the foci of an ellipse and B is an end of the minor axis. If STB is an equilateral triangle, then the eccentricity of the ellipse is
- a)
- b)
- c)
- d)
Answer:
Question: The length of the tangent drawn from any point on the circle x2 + y2 + 2fy + λ = 0 to the circle x2+ y2 + 2fy + μ = 0, where μ > λ > 0, is
- a)
- b)
- c)
- d) μ + λ
Answer:
Question: Find the eccentricity of the conic represented by x2 – y2 – 4x + 4y + 16 = 0
- a) 2
- b) √2
- c) 2 √2
- d) 3 √2
Answer: √2
Question: The length of the latus-rectum of the parabola whose focus is
and directrix is
is
- a)
- b)
- c)
- d)
Answer:
Question: The equation of the ellipse with focus at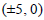 
and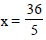 
as one directrix is
- a)
- b)
- c)
- d) None of these
Answer:
Question: For what value of k the circles x2 + y2 + 5x + 3y +7 = 0 and x2 + y2 – 8x + 6y + k = 0 cuts orthogonally
- a) 16
- b) –18
- c) – 13
- d) – 10
Answer: –18
Question: If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then the radius of the circle is
- a) 3/2
- b) 3/4
- c) 1/10
- d) 1/20
Answer: 3/4
Question: If the line 2x – 1 = 0 is the directrix of the parabola y2 – kx + 6 = 0 then one of the values of k is
- a) – 6
- b) 6
- c) 1/4
- d) – 1/4
Answer: – 6
Question: The line ax + by = 1 cuts ellipse cx2 + dy2 = 1 only once if
- a) ca 2 + db2 =1
- b)
- c)
- d) ac2 + bd2 = 1
Answer:
Question: Find the equation of chord of the circle x2 + y2= 8x bisected at the point (4, 3)
- a) y = 3
- b) y = 1
- c) y = 6
- d) y = 7
Answer: y = 3
Question: Find the vertex of the parabola x2 – 8y – x + 19 = 0.
- a)
- b)
- c)
- d)
Answer:
Question: Which of the following lines, is a normal to the parabola y2 = 16x ?
- a) y = x – 11 cosθ – 3 cos3θ
- b) y = x – 11 cosθ – cos3θ
- c) y = (x – 11) cosθ + cos3θ
- d) y = (x – 11) cosθ – cos3θ
Answer: y = (x – 11) cosθ – cos3θ
Question: For what value of λ does the line y = x + λ touches the ellipse 9x2 + 16y2 =144.
- a)
- b)
- c)
- d)
Answer:
Question: The length of the semi-latus rectum of an ellipse is one thrid of its major axis, its eccentricity would be
- a)
- b)
- c)
- d)
Answer:
Question: An equilateral triangle is inscribed in the circle x2 + y2 = a2 with one of the vertices at (a, 0). What is the equation of the side opposite to this vertex ?
- a) 2x – a = 0
- b) x + a = 0
- c) 2x + a = 0
- d) 3x – 2a = 0
Answer: 2x + a = 0
Question: The equation of one of the common tangents to the parabola y2 = 8x and x2 + y2 -12x + 4 = 0 is
- a) y = –x + 2
- b) y = x – 2
- c) y = x + 2
- d) None of these
Answer: y = x + 2
Question: The line joining (5, 0) to ( (10cos q, 10sin q) is divided internally in the ratio 2 : 3 at P. If θ varies, then the locus of P is
- a) A pair of straight
- b) A circle lines
- c) A straight line
- d) None of these
Answer: A circle lines
Question: The number of integral values of λ for which x2 + y2 + λx + (1- λ)y + 5 = 0 is the equation of a circle whose radius cannot exceed 5, is
- a) 14
- b) 18
- c) 16
- d) None of these
Answer: 16
Question: The lengths of the tangent drawn from any point on the circle 15x2 +15y2 - 48x + 64y = 0 to the two circles 5x2 + 5y2 – 24x + 32y + 75 = 0 and 5x2 + 5y2 – 48x + 64y + 300 = 0 are in the ratio of
- a) 1 : 2
- b) 18
- c) 16
- d) None of these
Answer: 1 : 2
Question: The length of the chord x + y = 3 intercepted by the circle x2 + y2 - 2x - 2y - 2 = 0 is
- a)
- b)
- c)
√14
- d)
Answer:
√14
Question: The locus of the point of intersection of two tangents to the parabola y2 = 4ax, which are at right angle to one another is
- a) x2 + y2 = a2
- b) ay2 =x
- c) x + a = 0
- d)
Answer: x + a = 0
Question: The parabola having its focus at (3, 2) and directrix along the y-axis has its vertex at
- a) (2, 2)
- b)
- c)
- d)
Answer:
Question: Let S be the focus of the parabola y2 = 8x and PQ be the common chord of the circle x2 + y2 – 2x – 4y = 0 and the given parabola. The area of ΔPQS is
- a) 4 sq units
- b) 3 sq units
- c) 2 sq units
- d) 8 sq units
Answer: 4 sq units
Question: The eccentricity of an ellipse, with its centre at the origin, is 1/2. If one of the directrices is x = 4 , then the equation of the ellipse is:[
- a) 4x2 + 3y2 = 1
- b) 3x2 + 4y2 = 12
- c) 4x2 + 3y2 = 12
- d) 3x2 + 4y2 = 1
Answer: 3x2 + 4y2 = 12
Question: Area of the circle in which a chord of length √2 makes an angle p/2 at the centre, is
- a) π/2 sq units
- b) 2π sq units
- c) π sq units
- d) π/4 sq units
Answer: π sq units
Question: The angle of intersection of the two circles x2 + y2 – 2x – 2y = 0 and x2 + y2 = 4, is
- a) 30º
- b) 60º
- c) 90º
- d) 45º
Answer: 45º
Question: An arch of a bridge is semi-elliptical with major axis horizontal. If the length the base is 9 meter and the highest part of the bridge is 3 meter from the horizontal; the best approximation of the height of the arch. 2 meter from the centre of the base is
- a) 11/4 m
- b) 8/3 m
- c) 7/2 m
- d) 2 m
Answer: 8/3 m
Question: A pair of tangents are drawn from the origin to the circle x2 + y2+ 20 (x + y) + 20 = 0, then the equation of the pair of tangent are
- a) x2 + y2 - 5xy = 0
- b) x2 + y2 + 2x + y = 0
- c) x2 + y2 – xy + 7 = 0
- d) 2x2 + 2y2 + 5xy = 0
Answer: 2x2 + 2y2 + 5xy = 0
More Study Material
BITSAT Full Syllabus Mathematics Conic Sections MCQs
We hope students liked the above MCQs for Conic Sections designed as per the latest syllabus for Full Syllabus Mathematics released by BITSAT. Students of Full Syllabus should download the Multiple Choice Questions and Answers in Pdf format and practice the questions and solutions given in above Full Syllabus Mathematics MCQs Questions on daily basis. All latest MCQs with answers have been developed for Mathematics by referring to the most important and regularly asked topics which the students should learn and practice to get better score in school tests and examinations. Studiestoday is the best portal for Full Syllabus students to get all latest study material free of cost.
MCQs for Mathematics BITSAT Full Syllabus Conic Sections
Expert teachers of studiestoday have referred to NCERT book for Full Syllabus Mathematics to develop the Mathematics Full Syllabus MCQs. If you download MCQs with answers for the above chapter daily, you will get higher and better marks in Full Syllabus test and exams in the current year as you will be able to have stronger understanding of all concepts. Daily Multiple Choice Questions practice of Mathematics and its study material will help students to have stronger understanding of all concepts and also make them expert on all critical topics. You can easily download and save all MCQs for Full Syllabus Mathematics also from www.studiestoday.com without paying anything in Pdf format. After solving the questions given in the MCQs which have been developed as per latest course books also refer to the NCERT solutions for Full Syllabus Mathematics designed by our teachers
Conic Sections MCQs Mathematics BITSAT Full Syllabus
All MCQs given above for Full Syllabus Mathematics have been made as per the latest syllabus and books issued for the current academic year. The students of Full Syllabus can refer to the answers which have been also provided by our teachers for all MCQs of Mathematics so that you are able to solve the questions and then compare your answers with the solutions provided by us. We have also provided lot of MCQ questions for Full Syllabus Mathematics so that you can solve questions relating to all topics given in each chapter. All study material for Full Syllabus Mathematics students have been given on studiestoday.
Conic Sections BITSAT Full Syllabus MCQs Mathematics
Regular MCQs practice helps to gain more practice in solving questions to obtain a more comprehensive understanding of Conic Sections concepts. MCQs play an important role in developing understanding of Conic Sections in BITSAT Full Syllabus. Students can download and save or print all the MCQs, printable assignments, practice sheets of the above chapter in Full Syllabus Mathematics in Pdf format from studiestoday. You can print or read them online on your computer or mobile or any other device. After solving these you should also refer to Full Syllabus Mathematics MCQ Test for the same chapter
BITSAT MCQs Mathematics Full Syllabus Conic Sections
BITSAT Full Syllabus Mathematics best textbooks have been used for writing the problems given in the above MCQs. If you have tests coming up then you should revise all concepts relating to Conic Sections and then take out print of the above MCQs and attempt all problems. We have also provided a lot of other MCQs for Full Syllabus Mathematics which you can use to further make yourself better in Mathematics
You can download the BITSAT MCQs for Full Syllabus Mathematics Conic Sections for latest session from StudiesToday.com
Yes, you can click on the links above and download topic wise MCQs Questions PDFs for Conic Sections Full Syllabus for Mathematics
Yes, the MCQs issued by BITSAT for Full Syllabus Mathematics Conic Sections have been made available here for latest academic session
You can easily access the links above and download the Conic Sections Full Syllabus MCQs Mathematics for each topic
There is no charge for the MCQs and their answers for Full Syllabus BITSAT Mathematics Conic Sections you can download everything free
Regular revision of MCQs given on studiestoday for Full Syllabus subject Mathematics Conic Sections can help you to score better marks in exams
Multiple Choice Questions (MCQs) for Conic Sections Full Syllabus Mathematics are objective-based questions which provide multiple answer options, and students are required to choose the correct answer from the given choices.