NCERT Solutions Class 11 Computer Science Data Representation have been provided below and is also available in Pdf for free download. The NCERT solutions for Class 11 Computer Science have been prepared as per the latest syllabus, NCERT books and examination pattern suggested in Class 11 by CBSE, NCERT and KVS. Questions given in NCERT book for Class 11 Computer Science are an important part of exams for Class 11 Computer Science and if answered properly can help you to get higher marks. Refer to more Chapter-wise answers for NCERT Class 11 Computer Science and also download more latest study material for all subjects. Data Representation is an important topic in Class 11, please refer to answers provided below to help you score better in exams
Data Representation Class 11 Computer Science NCERT Solutions
Class 11 Computer Science students should refer to the following NCERT questions with answers for Data Representation in Class 11. These NCERT Solutions with answers for Class 11 Computer Science will come in exams and help you to score good marks
Data Representation NCERT Solutions Class 11 Computer Science
NCERT Solutions for Class 11 Computer Science Data Representation Short Answer Type Questions
Question 1: Explain octal and hexadecimal number.
Answer: Octal (base 8) was previously a popular choice for representing digital circuit numbers in a form that is more compact than binary. Octal is sometimes abbreviated as oct. Octal counting goes as :
0,1, 2, 3,4, 5, 6, 7,10,11,12,13,14,15,16,17,20, 21 and so on.
Hexadecimal (base 16) is currently the most popular choice for representing digital circuit numbers in a form that is more compact than binary. Hexadecimal numbers are sometimes represented by preceding the value with ‘Ox’, as in 0x1 B84. Hexadecimal is sometimes abbreviated as hex. Hexadecimal counting goes :
0,1,2, 3,4,5, 6, 7, 8,9, A, B, C, D, E, F, and so on.
Question 2: Explain decimal and binary number.
Answer:
Decimal (base 10) is the way most human beings represent numbers. Decimal is sometimes abbreviated as dec. Decimal counting goes :
0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18 and so on.
Binary (base 2) is the natural way most digital circuits represent and manipulate numbers. Binary numbers are sometimes represented by preceding the value with ‘Ob’, as in Ob1O11. Binary is sometimes abbreviated as bin.
Binary counting goes as : 0,1,10,11,100,101,110,
111, 1000, 1oo1, 1010,1011, 11oo, 1101, 1110, 1111,10000,10001 and so on.
Question 3: Convert (259)10 to binary form.
Answer:
Step 1: Divide (259)10 successively by 2 until the quotient is 0:
259/2 = 129, remainder is 1
129/2 = 64, remainder is 1
64/2 = 32, remainder is 0
32/2 = 16, remainder is 0
16/2 = 8, remainder is 0
8/2 = 4, remainder is 0
4/2 = 2, remainder is 0
2/2 = 1, remainder is 0
1/2 = 0, remainder is 1
Step 2: Read from the bottom (MSB) to top (LSB) as 100000011.
So, 100000011 is the binary equivalent of decimal number 259 (Answer).
Question 4: Convert (17.35)10 to binary form.
Answer:
To convert integer 17 to binary, follow these steps:
Divide 17 by 2 keeping notice of the quotient and the remainder. Continue dividing the quotient by 2 until you get a quotient of zero.
Then just write out the remainders in the reverse order to get the equivalent binary number.
17 / 2 = 8 with remainder 1
8 / 2 = 4 with remainder 0
4 / 2 = 2 with remainder 0
2 / 2 = 1 with remainder 0
1 / 2 = 0 with remainder 1
Here is the answer to 17 decimal to binary number:
10001
For converting decimal fraction 0.35 to binary number, follow these steps:
Step 1: Multiply 0.35 by 2 keeping notice of the resulting integer and fractional part. Continue multiplying by 2 until you get a resulting fractional part equal to zero (we calcuclate upto ten digits).
Step 2: Then just write out the integer parts from the results of each multiplication to get equivalent binary number.
0.35 × 2 = 0 + 0.7
0.7 × 2 = 1 + 0.4
0.4 × 2 = 0 + 0.8
0.8 × 2 = 1 + 0.6
0.6 × 2 = 1 + 0.2
0.2 × 2 = 0 + 0.4
0.4 × 2 = 0 + 0.8
0.8 × 2 = 1 + 0.59999999999999
0.59999999999999 × 2 = 1 + 0.19999999999999
0.19999999999999 × 2 = 0 + 0.39999999999998
Here is the answer to 0.35 decimal to binary number:
0.0101100110
Therefore, decimal number 17.35 converted to binary is equal:
Question 5: Convert (39286)10 to octal form.
Answer:
To convert decimal number 39286 to octal, follow these steps:
Divide 39286 by 8 keeping notice of the quotient and the remainder.
Continue dividing the quotient by 8 until you get a quotient of zero.
Then just write out the remainders in the reverse order to get octal equivalent of decimal number 39286.
Using the above steps, here is the work involved in the solution for converting 39286 to octal number:
39286 / 8 = 4910 with remainder 6
4910 / 8 = 613 with remainder 6
613 / 8 = 76 with remainder 5
76 / 8 = 9 with remainder 4
9 / 8 = 1 with remainder 1
1 / 8 = 0 with remainder 1
Then just write down the remainders in the reverse order to get the answer, The decimal number 39286 converted to octal is therefore equal to :
(39286)10 = (114566)8
Question 6: Convert (0.2)10 to the binary form.
Answer: For converting decimal fraction 0.2 to binary number, follow these steps:
Multiply 0.2 by 2 keeping notice of the resulting integer and fractional part. Continue multiplying by 2 until you get a resulting fractional part equal to zero (we calcuclate upto ten digits).
Then just write out the integer parts from the results of each multiplication to get equivalent binary number.
0.2 × 2 = 0 + 0.4
0.4 × 2 = 0 + 0.8
0.8 × 2 = 1 + 0.6
0.6 × 2 = 1 + 0.2
0.2 × 2 = 0 + 0.4
0.4 × 2 = 0 + 0.8
0.8 × 2 = 1 + 0.6
0.6 × 2 = 1 + 0.2
0.2 × 2 = 0 + 0.40000000000001
0.40000000000001 × 2 = 0 + 0.80000000000001
Here is the answer to 0.2 decimal to binary number:
0.0011001100
Therefore, decimal number 0.2 converted to binary is equal:
Question 7: Convert (423.03125)10 to octal form.
Answer: Decimal 423 in octal conversion provides the detailed information on what is the octal equivalent of (423)10, and the step-by-step work for how to convert the decimal (base-10) number 423 to its octal (base-8) equivalent.
(423)10 in octal is equal to:
(423)10 = (?)8
Perform successive MOD-8 operation for decimal 423, and mark the initial remainder as LSB and the final remainder as MSB as like the below.
MOD-8 of 423 423 / 8 = 52 Remainder is 7 → LSB
MOD-8 of 52 52 / 8 = 6 Remainder is 4
MOD-8 of 6 6 / 8 = 0 Remainder is 6 → MSB
Arrange the remainders from MSB to LSB forms the octal equivalent of 423.
42310 = 6478
Hence,
423 in octal is 647
Question 8: Fill the correct entry.
Decimal Binary Octal
0 000 0
1 001 1
2 ? 2
3 Oil 3
4 100 4
5 101 5
? 110 6
7 ? ?
Answer:
Decimal Binary Octal
0 000 0
1 001 1
2 010 2
3 Oil 3
4 100 4
5 101 5
? 110 6
7 111 7
NCERT Solutions for Class 11 Computer Science Data Representation Long Answer Type Questios
Question 1:
Do as directed :
(a) Convert the Decimal number 781 to its Binary equivalent.
(b) Convert Binary number 101101.001 to its decimal equivalent.
(c) Convert Octal number 321.7 into its Binary equivalent.
Answer: (a)
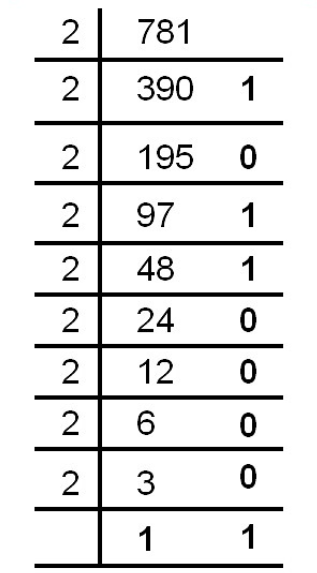
Therefore, 781 10 = 1100001101 2
(b) 101101.001 2 to its decimal equivalent
101101.001 = 1 x 2 5 + 0 x 2 4 + 1 x 2 3 + 1 x 2 2 + 0 x 2 1 + 1 x 2 0 + 0 x 2 -1 + 0 x 2 -2 + 1 x 2 -3
= 32 + 0 + 8 + 4 + 0 + 1 + 0 + 0 + 0.125
= 45.125 10
(c) 321.7 8 to its binary equivalent
3 2 1 7
011 010 001 111
Therefore, 321.7 8 = 11010001.111 2
Question 2: Do as directed :
(a) Covert the Hexadecimal number 3BC into its Binary equivalent
(b) Convert the Binary number 10011010.010101 to its Hexadecimal equivalent.
(c) Convert the Decimal number 345 into Octal number.
Answer: (a) 3BC 16 to its binary equivalent
3 B C
0011 1011 1100
Therefore, 3BC 16 = 001110111100 2
(b) 10011010.010101 2 to its hexadecimal equivalent
1001 1010 0101 0100
9 A 5 4
Therefore, 10011010.010101 2 = 9A.54 16
(c) 345 10 to its octal equivalent
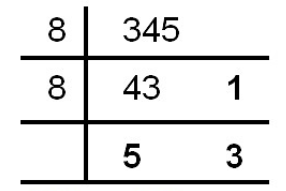
Therefore, 345 10 = 531 8
Question 3: Do as directed
(a) Convert the Decimal number 736 into Hexadecimal number.
(b) Convert the Octal number 246.45 into Hexadecimal number.
(c) Convert the Hexadecimal number ABF.C into Octal number.
(d) Covert the Octal number 576 to Decimal.
(e) Convert the Hexadecimal number A5C1 to Decimal,
Answer:
(a) To convert decimal number 736 to hexadecimal, follow these steps:
Divide736 by 16 keeping notice of the quotient and the remainder.
Continue dividing the quotient by 16 until you get a quotient of zero.
Then just write out the remainders in the reverse order to get hexadecimal equivalent of decimal number 736.
Using the above steps, here is the work involved in the solution for converting 736 to hexadecimal number:
736 / 16 = 46 with remainder 0
46 / 16 = 2 with remainder 14 (E)
2 / 16 = 0 with remainder 2
Then just write down the remainders in the reverse order to get the answer, The decimal number 736 converted to hexadecimal is therefore equal to :
2E0
(b) (246)8 = (A6)16
Step by step solution
Step 1: Look up each octal digit to obtain the equivalent group of three binary digits. You can use the table below to make these conversions.
Octal to Binary Conversion Table
Oct: 0 1 2 3 4 5 6 7
Bin: 000 001 010 011 100 101 110 111
(2)8 = (010)2
(4)8 = (100)2
(6)8 = (110)2
Step 2: Group each value of step 1 to make a binary number.
010 100 110
(246)8 = (10100110)2
Step 3: Now convert the binary number from step 2 to hexa by grouping all the digits of the binary in sets of four starting from the LSB (far right).
1010 0110
Note: add zeros to the left of the last digit if there aren't enough digits to make a set of four.
Step 4: Convert each group of four to the corresponding hexadecimal (use the table below),
1010=A, 0110=6.
So, 246 in octal is equivalent to A6 in hexadecimal
(d) To convert octal number 576 to decimal, follow these two steps:
Step 1: Start from one's place in 576 : multiply ones place with 8^0, tens place with 8^1, hundreds place with 8^2 and so on from right to left
Step 2: Add all the product we got from step 1 to get the decimal equivalent of 576.
Using the above steps, here is the work involved in the solution for converting 576 to decimal number (Don't forget that we start from ones place to so on...)
Decimal equivalent of "6" = 6 × 8^0 = 6
Decimal equivalent of "7" = 7 × 8^1 = 56
Decimal equivalent of "5" = 5 × 8^2 = 320
Decimal equivalent of "576" = 320566
576 = 382
Here is the final answer, The octal number 576 converted to decimal is therefore equal to:
382
(e) To convert hexadecimal number a5c1 to decimal, follow these two steps:
Step 1: Start from one's place in a5c1 : multiply ones place with 16^0, tens place with 16^1, hundreds place with 16^2 and so on from right to left
Step 2: Add all the product we got from step 1 to get the decimal equivalent of a5c1.
Using the above steps, here is the work involved in the solution for converting a5c1 to decimal number (Don't forget that we start from ones place to so on...)
Decimal equivalent of "1" = 1 × 16^0 = 1
Decimal equivalent of "c" = (c) 12 × 16^1 = 192
Decimal equivalent of "5" = 5 × 16^2 = 1280
Decimal equivalent of "a" = (a) 10 × 16^3 = 40960
Decimal equivalent of "a5c1" = 40960+1280+192+1
a5c1 = 42433
Here is the final answer, The hexadecimal number a5c1 converted to decimal is therefore equal to:
42433
Topic-2
Internal Storage Encoding Of Characters
NCERT Solutions for Class 11 Computer Science Data Representation Short Answer Type Questions-II
Question 1: What is ASCII ?
Answer: It is acronym for the American Standard Code for Information Interchange. It is used in most microcomputers and minicomputers and in many mainframes. It is a 7-bit code so it has 27 = 128 possible code groups.
Question 2: What is ISCII ?
Answer: It is acronym for Indian Standard Code for Information Interchange. It is a 8-bit code so it has 28 = 256 possible code groups. It retains all ASCII characters and offers coding for Indian characters also.
Question 3: What do you understand by Unicode ?
Answer: It is the new universal coding standard being adopted all newer platforms. Unicode provides a unique number for every character, no matter what the platform or program or the language is.
Question 4: Expand the following:
1. ASCII
2. ISCII
Answer:
1. ASCII: American Standard Code for Information Interchange.
2. ISCII : Indian Standard Code for Information Interchange. 2
| NCERT Solutions Class 11 Computer Science Chapter 1 Microprocessor and Memory Concepts |
| NCERT Solutions Class 11 Computer Science Chapter 1 Software Concepts |
| NCERT Solutions Class 11 Computer Science Chapter 7 Functions |
| NCERT Solutions Class 11 Computer Science Chapter 8 Strings |
| NCERT Solutions Class 11 Computer Science Chapter 10 Lists Dictionaries and Tuples |
NCERT Solutions Class 11 Computer Science Data Representation
The above provided NCERT Solutions Class 11 Computer Science Data Representation is available on our website for free download in Pdf. You can read the solutions to all questions given in your Class 11 Computer Science textbook online or you can easily download them in pdf. The answers to each question in Data Representation of Computer Science Class 11 has been designed based on the latest syllabus released for the current year. We have also provided detailed explanations for all difficult topics in Data Representation Class 11 chapter of Computer Science so that it can be easier for students to understand all answers. These solutions of Data Representation NCERT Questions given in your textbook for Class 11 Computer Science have been designed to help students understand the difficult topics of Computer Science in an easy manner. These will also help to build a strong foundation in the Computer Science. There is a combination of theoretical and practical questions relating to all chapters in Computer Science to check the overall learning of the students of Class 11.
You can download the NCERT Solutions for Class 11 Computer Science Data Representation for latest session from StudiesToday.com
Yes, the NCERT Solutions issued for Class 11 Computer Science Data Representation have been made available here for latest academic session
Regular revision of NCERT Solutions given on studiestoday for Class 11 subject Computer Science Data Representation can help you to score better marks in exams
Yes, studiestoday.com provides all latest NCERT Data Representation Class 11 Computer Science solutions based on the latest books for the current academic session
Yes, NCERT solutions for Class 11 Data Representation Computer Science are available in multiple languages, including English, Hindi
All questions given in the end of the chapter Data Representation have been answered by our teachers

