NCERT Solutions Class 12 Mathematics Chapter 3 Matrices have been provided below and is also available in Pdf for free download. The NCERT solutions for Class 12 Mathematics have been prepared as per the latest syllabus, NCERT books and examination pattern suggested in Class 12 by CBSE, NCERT and KVS. Questions given in NCERT book for Class 12 Mathematics are an important part of exams for Class 12 Mathematics and if answered properly can help you to get higher marks. Refer to more Chapter-wise answers for NCERT Class 12 Mathematics and also download more latest study material for all subjects. Chapter 3 Matrices is an important topic in Class 12, please refer to answers provided below to help you score better in exams
Chapter 3 Matrices Class 12 Mathematics NCERT Solutions
Class 12 Mathematics students should refer to the following NCERT questions with answers for Chapter 3 Matrices in Class 12. These NCERT Solutions with answers for Class 12 Mathematics will come in exams and help you to score good marks
Chapter 3 Matrices NCERT Solutions Class 12 Mathematics
Exercise 3.1
Find the value of the following:
Question: 1 (i) The order of the matrix,
(ii) The number of elements,
(iii) Write the elements a13, a21, a33, a24, a23.
Answer
(i) In the given matrix, the number of rows is 3 and the number of columns is 4. Therefore, the order of the matrix is 3 × 4.
(ii) Since the order of the matrix is 3 × 4, there are 3 × 4 = 12 elements in it.
(iii) a13 = 19, a21 = 35, a33 = −5, a24 = 12, a23 = 5/2
2. If a matrix has 24 elements, what are the possible orders it can have? What, if it has 13 elements?
Answer
We know that if a matrix is of the order m × n, it has mn elements. Thus, to find all the possible orders of a matrix having 24 elements, we have to find all the ordered pairs of natural numbers whose product is 24.
The ordered pairs are: (1, 24), (24, 1), (2, 12), (12, 2), (3, 8), (8, 3), (4, 6), and (6, 4)
Hence, the possible orders of a matrix having 24 elements are:
1 × 24, 24 × 1, 2 × 12, 12 × 2, 3 × 8, 8 × 3, 4 × 6, and 6 × 4
(1, 13) and (13, 1) are the ordered pairs of natural numbers whose product is 13.
Hence, the possible orders of a matrix having 13 elements are 1 × 13 and 13 × 1.
3. If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements?
Answer
We know that if a matrix is of the order m × n, it has mn elements. Thus, to find all the possible orders of a matrix having 18 elements, we have to find all the ordered pairs of natural numbers whose product is 18.
The ordered pairs are: (1, 18), (18, 1), (2, 9), (9, 2), (3, 6,), and (6, 3)
Hence, the possible orders of a matrix having 18 elements are:
1 × 18, 18 × 1, 2 × 9, 9 × 2, 3 × 6, and 6 × 3
(1, 5) and (5, 1) are the ordered pairs of natural numbers whose product is 5.
Hence, the possible orders of a matrix having 5 elements are 1 × 5 and 5 × 1.
4. Construct a 2 × 2 matrix, A = [aij], whose elements are given by:
Answer
5. Construct a 3 × 4 matrix, whose elements are given by:
(i) aij = 1/2 |-3 + j|
(ii) aij = 2i - j
Answer
(i) aij = 1/2 |-3 + j|
a11 = 1/2|−3 × 1 + 1| = 1/2|−3 + 1| = 1
a12 = 1/2|−3 × 1 + 2| = 1/2|−3 + 2| = 1/2
a13 = 1/2|−3 × 1 + 3| = 1/2|−3 + 3| = 0
a14 = 1/2|−3 × 1 + 4| = 1/2|−3 + 4| = 1/2
a21 = 1/2|−3 × 2 + 1| = 1/2|−6 + 1| = 5/2
a22 = 1/2|−3 × 2 + 2| = 1/2|−6 + 2| = 2
a23 = 1/2|−3 × 2 + 3| = 1/2|−6 + 3| = 3/2
a24 = 1/2|−3 × 2 + 4| = 1/2|−6 + 4| = 1
a31 = 1/2|−3 × 3 + 1| = 1/2|−9 + 1| = 4
a32 = 1/2|−3 × 3 + 2| = 1/2|−9 + 2| = 7/2
a33 = 1/2|−3 × 3 + 3| = 1/2|−9 + 3| = 3
a34 = 1/2|−3 × 3 + 4| = 1/2|−9 + 4| = 5/2
a11 = 2 × 1 − 1 = 2 −1 = 1
a12 = 2 × 1 − 2 = 2 −2 = 0
a13 = 2 × 1 − 3 = 2 −3 = -1
a14 = 2 × 1 − 4 = 2 −4 = -2
a21 = 2 × 2 − 1 = 4 −1 = 3
a22 = 2 × 2 − 2 = 4 −2 = 2
a23 = 2 × 2 − 3 = 4 −3 = 1
a24 = 2 × 2 − 4 = 4 −4 = 0
a31 = 2 × 3 − 1 = 6 −1 = 5
a32 = 2 × 3 − 2 = 6 −2 = 4
a33 = 2 × 3 − 3 = 6 −3 = 3
a34 = 2 × 3 − 4 = 6 −4 = 2
6. Find the values of x, y and z from the following equations:
Answer
(i)
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
x = 1, y = 4, and z = 3
(ii)
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we
get: x + y = 6, xy = 8, 5 + z = 5
Now, 5 + z = 5 ⇒ z = 0
we know that:
(x − y)2 = (x + y)2 − 4xy
⇒ (x − y)2 = 36 − 32 = 4
⇒ x − y = ±2
Now, when x − y = 2 and x + y = 6, we get x = 4 and y = 2
When x − y = − 2 and x + y = 6, we get x = 2 and y = 4
∴ x = 4, y = 2, and z = 0 or x = 2, y = 4, and z = 0
(iii)
As the two matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
x + y + z = 9 ... (1)
x + z = 5 ........ (2)
y + z = 7 ........ (3)
From (1) and (2), we have:
y + 5 = 9
⇒ y = 4
Then, from (3), we have:
4 + z = 7
⇒ z = 3
∴ x + z = 5
⇒ x = 2
∴ x = 2, y = 4 and z = 3.
7. Find the value of a, b, c and d from the equation:
Answer
As the two matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
a − b = −1 ...... (1)
2a − b = 0 ...... (2)
2a + c = 5 ....... (3)
3c + d = 13 ..... (4)
From (2), we have:
b = 2a
Then, from (1), we have:
a − 2a = −1 ⇒ a = 1 ⇒ b = 2
Now, from (3), we have:
2 ×1 + c = 5 ⇒ c = 3
From (4) we have:
3 × 3 + d = 13
⇒ 9 + d = 13 ⇒ d = 4
∴ a = 1, b = 2, c = 3 and d = 4.
8. A = [aij]mxn is a square matrix, if
(A) m < n
(B) m > n
(C) m = n
(D) None of these
Answer
The correct answer is C.
It is known that a given matrix is said to be a square matrix if the number of rows is equal to the number of columns.
Therefore, A =[aij]mxn is a square matrix, if m = n
9. Which of the given values of x and y make the following pair of matrices equal
(A) x = -1/3, y = 7
(B) Not possible to find
(C) y = 7, x = -2/3
(D) x = -1/3, y = -2/3
Answer
The correct answer is B.
It is given that,
Equating the corresponding elements, we get:
3x + 7 = 0 ⇒ x = -7/3 and 5 = y − 2 ⇒ y = 7
y + 1 = 8 ⇒ y = 7 and 2 − 3x = 4 ⇒ x = -2/3
We find that on comparing the corresponding elements of the two matrices, we get two different values of x, which is not possible.
Hence, it is not possible to find the values of x and y for which the given matrices are equal.
10. The number of all possible matrices of order 3 × 3 with each entry 0 or 1 is:
(A) 27
(B) 18
(C) 81
(D) 512
Answer
The correct answer is D.
The given matrix of the order 3 × 3 has 9 elements and each of these elements can be either 0 or 1.
Now, each of the 9 elements can be filled in two possible ways.
Therefore, by the multiplication principle, the required number of possible matrices is 29 = 512
Exercise 3.2
Question: 1
Find each of the following:
(i) A + B
(ii) A – B
(iii) 3A – C
(iv) AB
(v) BA
Answer
(i) A + B
2. Compute the following:
Answer
3. Compute the indicated products.
Answer
Question: 4
(A+B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
Answer
Question5. If
Question 6:
Answer
Question 7: Find X and Y, if
Answer
(i)
Question 8: Find X, if
Answer
Question 9: Find x and y, if
Answer
Question 10: Solve the equation for x, y, z and t if
Answer
Question 11:
Answer
Comparing the corresponding elements of these two matrices, we get:
2x − y = 10 and 3x + y = 5
Adding these two equations, we have:
5x = 15
⇒ x = 3
Now, 3x + y = 5
⇒ y = 5 − 3x
⇒ y = 5 − 9 = −4
∴x = 3 and y = −4
Question 12: Given
Answer
Question 13:
Answer
Question 14: Show that
Answer
Question 15: Find
Answer
We have A2 = A × A
Question 16:
Answer
Question 17:
Answer
Comparing the corresponding elements, we have:
3K - 2 = 1
⇒ 3K = 3
⇒ K = 1
Thus, the value of k is 1.
Question 18:
Answer
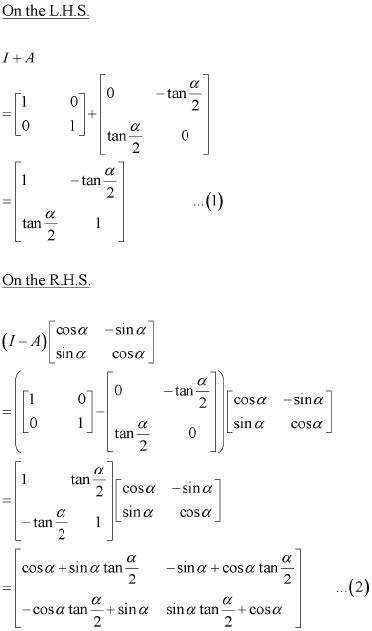
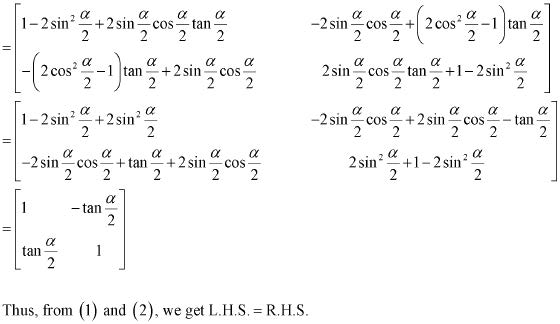
Question 19: A trust fund has Rs 30,000 that must be invested in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication, determine how to divide Rs 30,000 among the two types of bonds. If the trust fund must obtain an annual total interest of:
(a) Rs 1,800 (b) Rs 2,000
Answer
(a) Let Rs x be invested in the first bond. Then, the sum of money invested in the second bond will be Rs (30000 − x).
It is given that the first bond pays 5% interest per year and the second bond pays 7% interest per year.
Therefore, in order to obtain an annual total interest of Rs 1800, we have
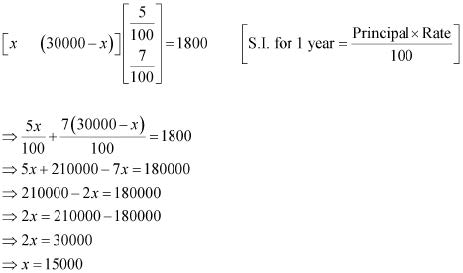
Thus, in order to obtain an annual total interest of Rs 1800, the trust fund should invest
Rs 15000 in the first bond and the remaining Rs 15000 in the second bond.
(b) Let Rs x be invested in the first bond. Then, the sum of money invested in the second bond will be Rs (30000 − x).
Therefore, in order to obtain an annual total interest of Rs 2000, we have:
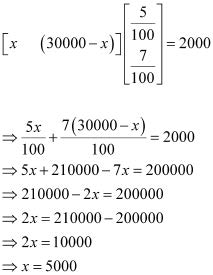
Thus, in order to obtain an annual total interest of Rs 2000, the trust fund should invest Rs 5000 in the first bond and the remaining Rs 25000 in the second bond.
Question20. The bookshop of a particular school has 10 dozen chemistry books, 8 dozen physics books, 10 dozen economics books. Their selling prices are ` 80, ` 60 and ` 40 each respectively. Find the total amount the bookshop will receive from selling all the books using matrix algebra.
Solution :
The bookshop has 10 dozen chemistry books, 8 dozen physics books, and 10 dozen economics books.
The selling prices of a chemistry book, a physics book, and an economics book are respectively given as Rs 80, Rs 60, and Rs 40.
The total amount of money that will be received from the sale of all these books can be represented in the form of a matrix as:
Question21. Assume X, Y, Z, W and P are matrices of order 2 x n,3 x k,2 x p, n x 3 and p x k repectively. The restriction on n,k and p so that PY + WY will be define are:
A. k = 3, p = n
B. k is arbitrary, p = 2
C. p is arbitrary, k = 3
D. k = 2, p = 3
Solution :
Matrices P and Y are of the orders p × k and 3 × k respectively.
Therefore, matrix PY will be defined if k = 3. Consequently, PY will be of the order p × k.
Matrices W and Y are of the orders n × 3 and 3 × k respectively.
Since the number of columns in W is equal to the number of rows in Y, matrix WY is well-defined and is of the order n × k.
Matrices PY and WY can be added only when their orders are the same.
However, PY is of the order p × k and WY is of the order n × k. Therefore, we must have p = n.
Thus, k = 3 and p = n are the restrictions on n, k, and p so that PY + WY will be defined.
Question22. Assume X, Y, Z, W and P are matrices of order 2 x n,3 x k,2 x p, n x 3 and p x k repectively. If n = p then order of matrix 7X – 5Z is:
(A) p × 2
(B) 2 × n
(C) n × 3
(D)p × n
Solution :
Matrix X is of the order 2 × n.
Therefore, matrix 7X is also of the same order.
Matrix Z is of the order 2 × p, i.e., 2 × n [Since n = p]
Therefore, matrix 5Z is also of the same order.
Now, both the matrices 7X and 5Z are of the order 2 × n.
Thus, matrix 7X − 5Z is well-defined and is of the order 2 × n.
Exercise 3.3
Question 1: Find the transpose of each of the following matrices:
Answer
Question 2:
Answer
We have:
Question 3:
(i) It is known that
Therefore, we have:
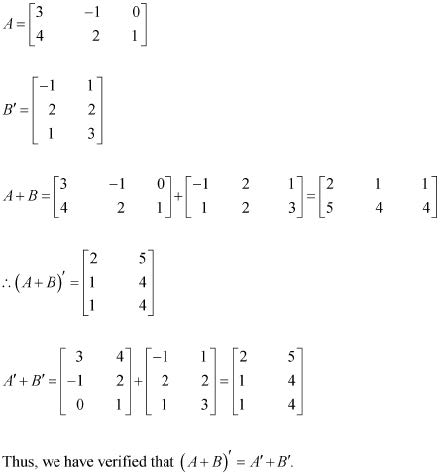
Question 4:
| NCERT Solutions Class 12 Mathematics Chapter 1 Relations and Functions |
| NCERT Solutions Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions |
| NCERT Solutions Class 12 Mathematics Chapter 3 Matrices |
| NCERT Solutions Class 12 Mathematics Chapter 4 Determinants |
| NCERT Solutions Class 12 Mathematics Chapter 5 Continuity and Differentiability |
| NCERT Solutions Class 12 Mathematics Chapter 6 Application of Derivatives |
| NCERT Solutions Class 12 Mathematics Chapter 7 Integrals |
| NCERT Solutions Class 12 Mathematics Chapter 8 Application of Integrals |
| NCERT Solutions Class 12 Mathematics Chapter 9 Differential Equations |
| NCERT Solutions Class 12 Mathematics Chapter 10 Vector Algebra |
| NCERT Solutions Class 12 Mathematics Chapter 11 Three Dimensional Geometry |
| NCERT Solutions Class 12 Mathematics Chapter 12 Linear Programming |
| NCERT Solutions Class 12 Mathematics Chapter 13 Probability |
NCERT Solutions Class 12 Mathematics Chapter 3 Matrices
The above provided NCERT Solutions Class 12 Mathematics Chapter 3 Matrices is available on our website for free download in Pdf. You can read the solutions to all questions given in your Class 12 Mathematics textbook online or you can easily download them in pdf. The answers to each question in Chapter 3 Matrices of Mathematics Class 12 has been designed based on the latest syllabus released for the current year. We have also provided detailed explanations for all difficult topics in Chapter 3 Matrices Class 12 chapter of Mathematics so that it can be easier for students to understand all answers. These solutions of Chapter 3 Matrices NCERT Questions given in your textbook for Class 12 Mathematics have been designed to help students understand the difficult topics of Mathematics in an easy manner. These will also help to build a strong foundation in the Mathematics. There is a combination of theoretical and practical questions relating to all chapters in Mathematics to check the overall learning of the students of Class 12.
You can download the NCERT Solutions for Class 12 Mathematics Chapter 3 Matrices for latest session from StudiesToday.com
Yes, the NCERT Solutions issued for Class 12 Mathematics Chapter 3 Matrices have been made available here for latest academic session
Regular revision of NCERT Solutions given on studiestoday for Class 12 subject Mathematics Chapter 3 Matrices can help you to score better marks in exams
Yes, studiestoday.com provides all latest NCERT Chapter 3 Matrices Class 12 Mathematics solutions based on the latest books for the current academic session
Yes, NCERT solutions for Class 12 Chapter 3 Matrices Mathematics are available in multiple languages, including English, Hindi
All questions given in the end of the chapter Chapter 3 Matrices have been answered by our teachers

